What is Kernel in Machine Learning?
Serdar Palaoglu

In the realm of machine learning, kernels hold a pivotal role, especially in algorithms designed for classification and regression tasks like Support Vector Machines (SVMs). The kernel function is the heart of these algorithms, adept at simplifying the complexity inherent in data. It transforms non-linear relationships into a linear format, making them accessible for algorithms that traditionally only handle linear data.
This transformation is important for allowing SVMs to unravel and make sense of complex patterns and relationships. Kernels achieve this without the computational intensity of mapping data to higher dimensions explicitly. Their efficiency and effectiveness in revealing hidden patterns make them a cornerstone in modern machine learning.
As we explore kernels further, we uncover their significance in enhancing the performance and applicability of SVMs in diverse scenarios.
Note: If you are interested in a 30min conversation with one of our Machine Learning experts regarding the topic of kernels in machine learning, please take a look at our ML expert talk offering.
What is Kernel in Machine Learning?
The concept of a kernel in machine learning offers a compelling and intuitive way to understand this powerful tool used in Support Vector Machines (SVMs). At its most fundamental level, a kernel is a relatively straightforward function that operates on two vectors from the input space, commonly referred to as the X space. The primary role of this function is to return a scalar value, but the fascinating aspect of this process lies in what this scalar represents and how it is computed.
This scalar is, in essence, the dot product of the two input vectors. However, it's not computed in the original space of these vectors. Instead, it's as if this dot product is calculated in a much higher-dimensional space, known as the Z space. This is where the kernel's true power and elegance come into play. It manages to convey how close or similar these two vectors are in the Z space without the computational overhead of actually mapping the vectors to this higher-dimensional space and calculating their dot product there.
The kernel thus serves as a kind of guardian of the Z space. It allows you to glean the necessary information about the vectors in this more complex space without having to access the space directly. This approach is particularly useful in SVMs, where understanding the relationship and position of vectors in a higher-dimensional space is crucial for classification tasks.

Professor Abu-Mostafa's analogy
Imagine the high-dimensional space (Z space) in machine learning as a secret room full of complex information. If you wanted to fully understand a vector (a point or a set of values) in this room, it would mean opening the door and getting all the complex details about it. This is like asking for the transformed version of an input vector – it's complicated and reveals a lot about the secret room.
However, what if you didn't need to know everything about the vector in the secret room, but just needed to know how similar or different two vectors are? This is where the kernel function comes in. The kernel function is like a helpful assistant who can go into the secret room (Z space) and do this comparison for you. You give the kernel two vectors from the original space (X space), and it goes into the Z space, does the calculations, and comes back with just a single number. This number tells you how similar the two vectors are in the high-dimensional Z space.
The beauty of this is that you get the information you need (the similarity measure) without having to deal with the complexity of the Z space yourself. It's like getting a simple answer from the assistant without having to go into the room and figure out everything on your own. This makes things much easier and more efficient, especially in complex machine-learning tasks.
This efficiency and simplicity of the kernel function are what make it a powerful tool in machine learning, particularly for SVMs. It allows these models to operate as though they are working in a higher-dimensional space, capturing more complex relationships in the data, all while avoiding the direct computational complexities associated with such high-dimensional calculations.
What Is the Kernel Trick?
The "Kernel Trick" is a clever technique in machine learning that allows algorithms, especially those used in Support Vector Machines (SVMs), to operate in a high-dimensional space without directly computing the coordinates in that space. The reason it's called a "trick" is because it cleverly circumvents the computationally intensive task of mapping data points into a higher-dimensional space, which is often necessary for making complex, non-linear classifications.
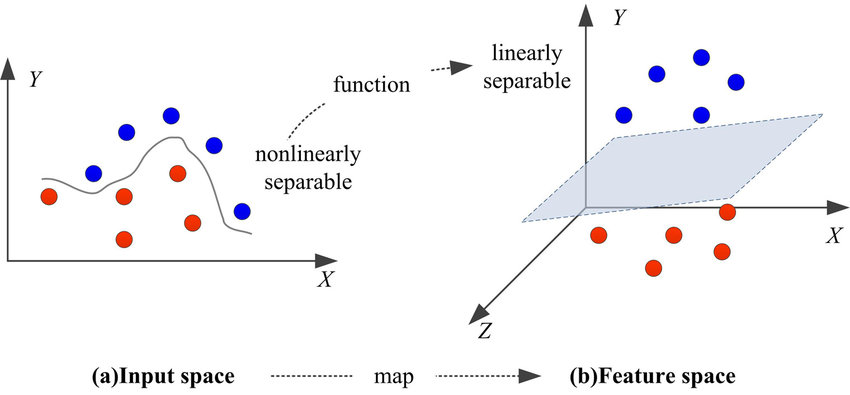
How Kernels Work in Practice?
Firstly, a kernel takes the data from its original space and implicitly maps it to a higher-dimensional space. This is crucial when dealing with data that is not linearly separable in its original form. Instead of performing computationally expensive high-dimensional calculations, the kernel function calculates the relationships or similarities between pairs of data points as if they were in this higher-dimensional space.
This calculation of similarities is fundamental to how kernels facilitate complex classifications. In the context of SVMs, for instance, the kernel function computes the dot product of input data pairs in the transformed space. This process effectively determines the relationships between data points, allowing the SVM to find separating hyperplanes (boundaries) that can categorize data points into different classes, even when such categorization isn't apparent in the original space.
How to Choose a Kernel?
Choosing the right kernel for a machine learning task, such as in Support Vector Machines (SVMs), is a critical decision that can significantly impact the performance of the model. The selection process involves understanding both the nature of the data and the specific requirements of the task at hand.
Firstly, it's important to consider the distribution and structure of the data. If the data is linearly separable, a linear kernel may be sufficient. However, for more complex, non-linear data, a polynomial or radial basis function (RBF) kernel might be more appropriate.
The polynomial kernel, for example, is effective for datasets where the relationship between variables is not merely linear but involves higher-degree interactions. On the other hand, the RBF kernel, often a go-to choice, is particularly useful for datasets where the decision boundary is not clear, and the data points form more of a cloud-like structure.
Another crucial aspect is the tuning of kernel parameters, which can drastically influence the model's accuracy. For instance, in the RBF kernel, the gamma parameter defines how far the influence of a single training example reaches, with low values meaning ‘far’ and high values meaning ‘close’. The correct setting of these parameters often requires iterative experimentation and cross-validation to avoid overfitting and underfitting.
In practical scenarios, it's also advisable to consider computational efficiency. Some kernels might lead to quicker convergence and less computational overhead, which is essential in large-scale applications or when working with vast datasets.
Lastly, domain knowledge can play a significant role in kernel selection. Understanding the underlying phenomena or patterns in the data can guide the choice of the kernel. For example, in text classification or natural language processing, certain kernels might be more effective in capturing the linguistic structures and nuances.
Conclusion
In summary, kernels in machine learning embody a crucial technique for handling complex, non-linear data in a computationally efficient manner. They enable algorithms, particularly SVMs, to operate in high-dimensional spaces without the direct computation of these dimensions, simplifying the analysis of intricate data patterns. This implicit mapping to higher dimensions allows for more accurate and sophisticated data classification and regression tasks.
The versatility and computational efficiency of kernels make them a cornerstone in the field of machine learning, contributing significantly to advancements in technology, healthcare, finance, and beyond. As we continue to explore and refine these tools, the potential for kernels to unlock deeper insights and solutions in various domains remains immense and largely untapped.
Frequently Asked Questions
Can kernel methods be used for supervised problems?
Yes, kernel methods can be used for both supervised and unsupervised learning problems. In supervised learning, they are prominently used in algorithms like Support Vector Machines (SVMs) for tasks such as classification and regression. In unsupervised learning, they find applications in methods like kernel spectral clustering, aiding in the identification of inherent groupings within data.
What are quantum kernel methods?
Quantum kernel methods are an emerging area in quantum machine learning, where kernel functions are computed using a quantum feature map. This approach leverages the computational capabilities of quantum systems to process complex, high-dimensional data more efficiently, potentially offering significant advantages over classical kernel methods, especially in terms of speed and handling large datasets.
What are the three types of kernels?
In computing architecture, kernels are classified into three main types: monolithic, microkernel, and hybrid. Monolithic kernels integrate all system services in one large kernel, offering high performance but at the risk of potential system instability. Microkernels keep only the essential services within the kernel, enhancing modularity and system stability. Hybrid kernels blend characteristics of both monolithic and microkernel architectures, seeking a balance between performance and stability.
Contact
If you would like to speak with us about this topic, please reach out and we will schedule an introductory meeting right away.
