Was ist ein Kernel beim maschinellen Lernen?

Das Konzept des Kernels im maschinellen Lernen bietet eine überzeugende und intuitive Möglichkeit, dieses leistungsstarke Werkzeug zu verstehen, das in Support Vector Machines (SVMs) verwendet wird. Auf seiner grundlegendsten Ebene ist ein Kernel eine relativ einfache Funktion, die auf zwei Vektoren aus dem Eingaberaum, allgemein als X-Raum bezeichnet, wirkt. Die primäre Aufgabe dieser Funktion besteht darin, einen Skalarwert zurückzugeben, aber der faszinierende Aspekt dieses Prozesses liegt darin, was dieser Skalarwert darstellt und wie er berechnet wird.

Dieser Skalarwert ist im Wesentlichen das Punktprodukt der beiden Eingangsvektoren. Es wird jedoch nicht im ursprünglichen Raum dieser Vektoren berechnet. Stattdessen ist es so, als ob dieses Punktprodukt in einem viel höher-dimensionalen Raum, dem so genannten Z-Raum, berechnet wird. Hier kommen die wahre Stärke und Eleganz des Kernels ins Spiel. Er vermittelt, wie nahe oder ähnlich sich diese beiden Vektoren im Z-Raum sind, ohne den Rechenaufwand, die Vektoren in diesen höherdimensionalen Raum abzubilden und dort ihr Punktprodukt zu berechnen.

Der Kernel dient somit als eine Art Wächter des Z-Raums. Er ermöglicht es Ihnen, die notwendigen Informationen über die Vektoren in diesem komplexeren Raum zu sammeln, ohne direkt auf den Raum zugreifen zu müssen. Dieser Ansatz ist besonders bei SVMs nützlich, wo das Verständnis der Beziehung und der Position von Vektoren in einem höherdimensionalen Raum für Klassifizierungsaufgaben entscheidend ist.

Die Analogie von Professor Abu-Mostafa

Stellen Sie sich den hochdimensionalen Raum (Z-Raum) beim maschinellen Lernen als einen geheimen Raum voller komplexer Informationen vor. Wenn Sie einen Vektor (einen Punkt oder eine Reihe von Werten) in diesem Raum vollständig verstehen wollten, müssten Sie die Tür öffnen und alle komplexen Details darüber erfahren. Das ist so, als würde man nach der transformierten Version eines Eingabevektors fragen - das ist kompliziert und verrät eine Menge über den geheimen Raum.

Was aber, wenn man nicht alles über den Vektor im geheimen Raum wissen muss, sondern nur wissen will, wie ähnlich oder unterschiedlich zwei Vektoren sind? An dieser Stelle kommt die Kernel-Funktion ins Spiel. Die Kernel-Funktion ist wie ein hilfreicher Assistent, der in den geheimen Raum (Z-Raum) gehen kann und diesen Vergleich für Sie durchführt. Sie geben dem Kernel zwei Vektoren aus dem ursprünglichen Raum (X-Raum), und er geht in den Z-Raum, führt die Berechnungen durch und kommt mit nur einer einzigen Zahl zurück. Diese Zahl sagt Ihnen, wie ähnlich die beiden Vektoren im hochdimensionalen Z-Raum sind.

Das Schöne daran ist, dass Sie die benötigten Informationen (das Ähnlichkeitsmaß) erhalten, ohne sich selbst mit der Komplexität des Z-Raums befassen zu müssen. Es ist, als würde man eine einfache Antwort von einem Assistenten erhalten, ohne dass man in den Raum gehen und alles selbst herausfinden muss. Das macht die Dinge viel einfacher und effizienter, insbesondere bei komplexen Aufgaben des maschinellen Lernens.

Diese Effizienz und Einfachheit der Kernel-Funktion machen sie zu einem leistungsstarken Werkzeug für das maschinelle Lernen, insbesondere für SVMs. Sie ermöglicht es diesen Modellen, so zu arbeiten, als würden sie in einem höherdimensionalen Raum arbeiten und komplexere Beziehungen in den Daten erfassen, während sie gleichzeitig die mit solchen hochdimensionalen Berechnungen verbundenen direkten Rechenkomplexitäten vermeiden.

Der "Kernel-Trick" ist eine Technik im Bereich des maschinellen Lernens, die es Algorithmen, insbesondere den in Support Vector Machines (SVMs) verwendeten, ermöglicht, in einem hochdimensionalen Raum zu arbeiten, ohne die Koordinaten in diesem Raum direkt zu berechnen. Der Grund dafür, dass er als "Trick" bezeichnet wird, liegt darin, dass er die rechenintensive Aufgabe der Abbildung von Datenpunkten in einen höherdimensionalen Raum umgeht, die häufig für komplexe, nichtlineare Klassifizierungen erforderlich ist.

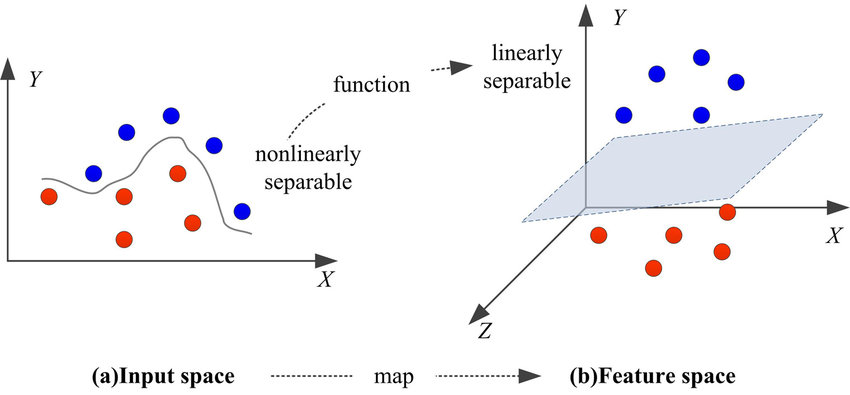
Zunächst nimmt ein Kernel die Daten aus ihrem ursprünglichen Raum und bildet sie implizit auf einen höherdimensionalen Raum ab. Dies ist von entscheidender Bedeutung, wenn es um Daten geht, die in ihrer ursprünglichen Form nicht linear trennbar sind. Anstatt rechenintensive hochdimensionale Berechnungen durchzuführen, berechnet die Kernel-Funktion die Beziehungen oder Ähnlichkeiten zwischen Datenpunktpaaren, als ob sie sich in diesem höherdimensionalen Raum befänden.

Diese Berechnung von Ähnlichkeiten ist grundlegend dafür, wie Kernels komplexe Klassifizierungen ermöglichen. Im Zusammenhang mit SVMs zum Beispiel berechnet die Kernel-Funktion das Punktprodukt von Eingabedatenpaaren im transformierten Raum. Dieser Prozess bestimmt effektiv die Beziehungen zwischen Datenpunkten und ermöglicht es der SVM, trennende Hyperebenen (Grenzen) zu finden, die Datenpunkte in verschiedene Klassen einteilen können, selbst wenn eine solche Einteilung im ursprünglichen Raum nicht offensichtlich ist.

Die Wahl des richtigen Kernels für eine Aufgabe des maschinellen Lernens, wie z. B. bei Support Vector Machines (SVMs), ist eine wichtige Entscheidung, die die Leistung des Modells erheblich beeinflussen kann. Der Auswahlprozess erfordert ein Verständnis sowohl der Art der Daten als auch der spezifischen Anforderungen der jeweiligen Aufgabe.

Zunächst einmal ist es wichtig, die Verteilung und Struktur der Daten zu berücksichtigen. Wenn die Daten linear trennbar sind, kann ein linearer Kernel ausreichend sein. Für komplexere, nicht lineare Daten kann jedoch ein Polynom- oder Radialbasisfunktionskernel (RBF) besser geeignet sein.

Der Polynom-Kernel eignet sich zum Beispiel für Datensätze, bei denen die Beziehung zwischen den Variablen nicht nur linear ist, sondern auch Wechselwirkungen höheren Grades aufweist. Andererseits ist der RBF-Kernel, der häufig gewählt wird, besonders nützlich für Datensätze, bei denen die Entscheidungsgrenze nicht eindeutig ist und die Datenpunkte eher eine wolkenartige Struktur bilden.

Ein weiterer entscheidender Aspekt ist die Abstimmung der Kernelparameter, die die Genauigkeit des Modells drastisch beeinflussen können. Beim RBF-Kernel beispielsweise definiert der Gamma-Parameter, wie weit der Einfluss eines einzelnen Trainingsbeispiels reicht, wobei niedrige Werte "weit" und hohe Werte "nah" bedeuten. Die korrekte Einstellung dieser Parameter erfordert oft iterative Experimente und Kreuzvalidierung, um eine Über- oder Unteranpassung zu vermeiden.

In praktischen Szenarien ist es auch ratsam, die Berechnungseffizienz zu berücksichtigen. Einige Kernel können zu einer schnelleren Konvergenz und einem geringeren Rechenaufwand führen, was bei umfangreichen Anwendungen oder bei der Arbeit mit großen Datensätzen wichtig ist.

Schließlich kann auch das Fachwissen eine wichtige Rolle bei der Auswahl des Kernels spielen. Das Verständnis der zugrundeliegenden Phänomene oder Muster in den Daten kann die Wahl des Kernels leiten. Bei der Textklassifizierung oder der Verarbeitung natürlicher Sprache beispielsweise können bestimmte Kernel die sprachlichen Strukturen und Nuancen besser erfassen.

Zusammenfassend lässt sich sagen, dass Kernel im Bereich des maschinellen Lernens eine entscheidende Technik für die recheneffiziente Verarbeitung komplexer, nichtlinearer Daten darstellen. Sie ermöglichen es Algorithmen, insbesondere SVMs, in hochdimensionalen Räumen zu operieren, ohne dass diese Dimensionen direkt berechnet werden müssen, was die Analyse komplizierter Datenmuster vereinfacht. Diese implizite Abbildung auf höhere Dimensionen ermöglicht genauere und anspruchsvollere Datenklassifizierungs- und Regressionsaufgaben.

Die Vielseitigkeit und Recheneffizienz von Kernels machen sie zu einem Eckpfeiler im Bereich des maschinellen Lernens und tragen maßgeblich zu Fortschritten in den Bereichen Technologie, Gesundheitswesen, Finanzen und darüber hinaus bei. Während wir diese Tools weiter erforschen und verfeinern, bleibt das Potenzial von Kernels, tiefere Einblicke und Lösungen in verschiedenen Bereichen zu erschließen, immens und weitgehend ungenutzt.

Können Kernel-Methoden für überwachte Probleme verwendet werden?

Ja, Kernel-Methoden können sowohl für überwachte als auch für unüberwachte Lernprobleme eingesetzt werden. In überwachtem Lernen werden sie prominent in Algorithmen wie Support Vector Machines (SVMs) für Aufgaben wie Klassifikation und Regression verwendet. In unüberwachtem Lernen finden sie Anwendung in Methoden wie der kernelbasierten spektralen Clusteranalyse, die bei der Identifizierung inhärenter Gruppierungen in Daten hilft.

Was sind Quanten-Kernel-Methoden?

Quanten-Kernel-Methoden sind ein aufkommendes Gebiet im Bereich des quantenbasierten maschinellen Lernens, bei dem Kernel-Funktionen mithilfe einer quantenbasierten Merkmalszuordnung berechnet werden. Dieser Ansatz nutzt die Rechenleistung von Quantensystemen effizienter, um komplexe, hochdimensionale Daten zu verarbeiten. Das bietet potenziell erhebliche Vorteile gegenüber klassischen Kernel-Methoden, insbesondere in Bezug auf Geschwindigkeit und Handhabung großer Datensätze.

Was sind die drei Arten von Kernels?

In der Computerarchitektur werden Kernel in drei Haupttypen eingeteilt: monolithisch, microkernel und hybridkernel. Monolithische Kernel integrieren alle Systemdienste in einem großen Kernel und bieten hohe Leistung, aber mit dem Risiko potenzieller Systeminstabilität. Mikrokernel behalten nur die wesentlichen Dienste im Kernel bei, verbessern die Modularität und Systemstabilität. Hybridkernel kombinieren Merkmale sowohl von monolithischen als auch von Mikrokernelarchitekturen und streben einen Ausgleich zwischen Leistung und Stabilität an.