Kollaboratives Filtern für Empfehlungsdienste

Das Ziel eines kollaborativen Filtersystems besteht darin, aus der Interaktion anderer Benutzer mit ähnlichem Geschmack mit einem bestimmten Objekt zu schließen, wie der Benutzer mit diesem Objekt interagieren könnte. Die Ähnlichkeit zwischen Nutzern kann auf verschiedene Weise ausgedrückt werden und kann auch verschiedene Merkmale der Nutzer berücksichtigen. Im Kontext des rein kollaborativen Filterns, das wir in diesem Artikel betrachten werden, wird ein Benutzer nur durch die Art und Weise beschrieben, wie er mit den Objekten interagiert hat.

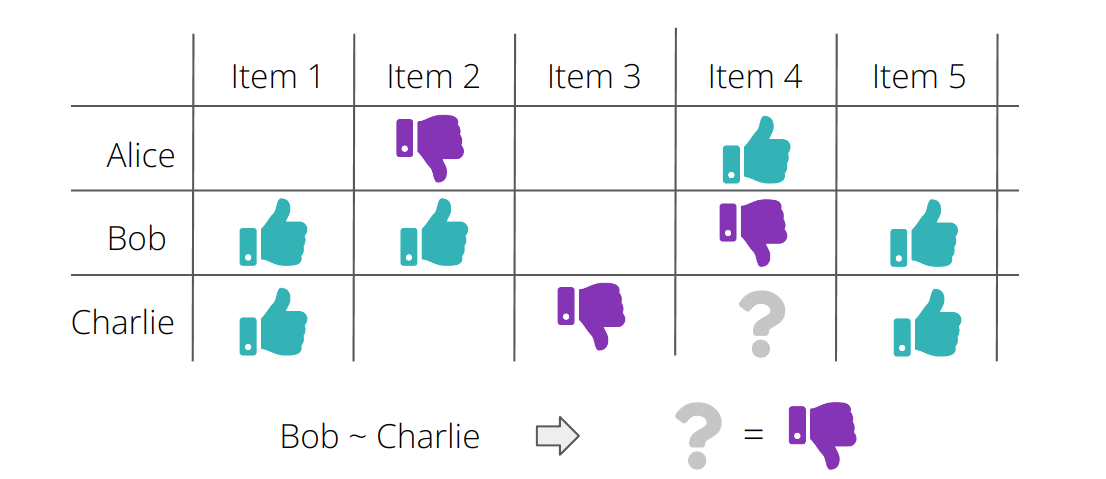
Es gibt viele interessante Möglichkeiten, wie man dies mathematisch formalisieren kann, und wir werden uns einige davon ansehen. Doch zunächst wollen wir uns den Datensatz, mit dem wir arbeiten werden, genauer untersuchen

Der MovieLens100k-Datensatz besteht aus 100.000 Benutzer-Film-Bewertungspaaren von 943 Benutzern für 1682 Filme. In seiner Rohform, ohne Informationen über die Nutzer und Filme, sieht er wie folgt aus:

Wie so oft bei solchen Datensätzen haben die meisten Filme nur sehr wenige Bewertungen und die meisten Nutzer haben nur eine sehr kleine Anzahl von Filmen bewertet.

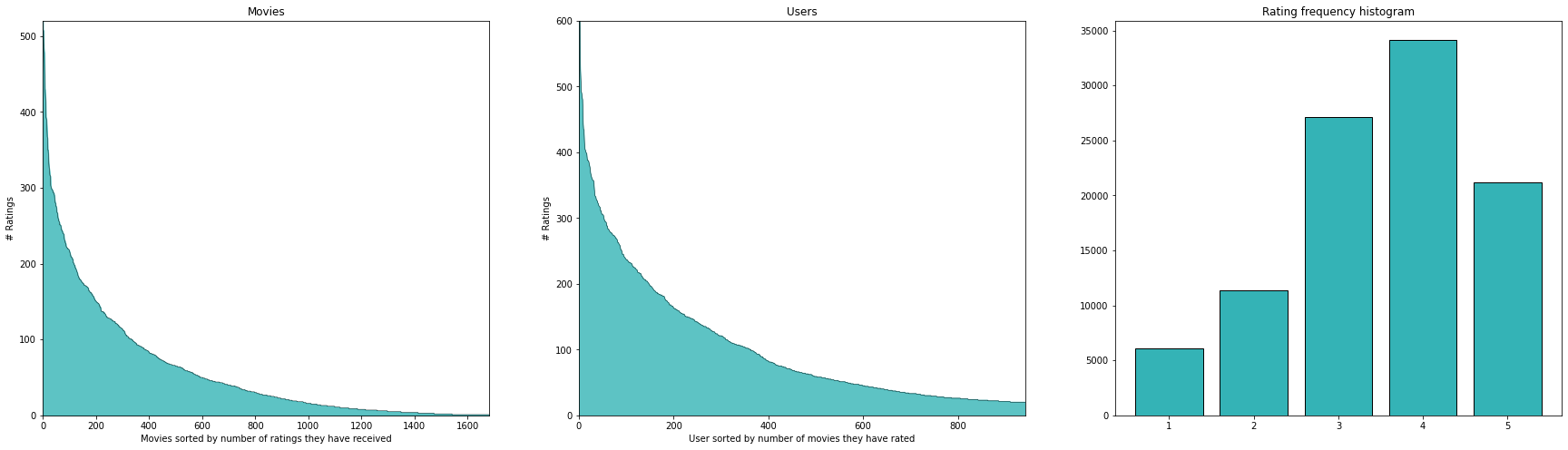
Wie wir aus den Diagrammen in der obigen Abbildung ersehen können, haben die meisten Filme eine geringe Anzahl von Bewertungen und ebenso haben die meisten Nutzer nur sehr wenige Artikel bewertet. Dies ist bei Empfehlungssystemen sehr häufig der Fall. Beachten Sie, dass es 1586126 ( = 943 * 1682) mögliche Interaktionen zwischen Nutzern und Filmen gibt, von denen jedoch nur 100k tatsächlich eine Bewertung haben - das sind nur ~ 6,3 %! Die Tatsache, dass es eine Handvoll Filme gibt, die die meisten Bewertungen erhalten, und dass es viele Filme mit nur sehr wenigen Bewertungen gibt, wird auch als long tail Phänomen bezeichnet.

Man kann es auch so ausdrücken, dass die Nutzer-Film-Matrix sehr dünn besetzt (sparse) ist. Bei größeren Datensätzen wäre die folgende Darstellung nicht wirklich machbar, aber mit dem mäßig großen Datensatz, mit dem wir arbeiten, können wir einen Blick auf die User-Movie-Matrix werfen.

Dabei stehen die Zeilen für die Filme und die Spalten für die Benutzer. Der Eintrag (oder das Pixel) an der Position $$(i,j)$$ wird entsprechend der Bewertung gefärbt, die Benutzer $$i$$ dem Film $$j$$ gegeben hat. Oder er ist weiß, wenn der Benutzer diesen Film nicht bewertet hat. Wir können uns auch einen kleinen Ausschnitt ansehen:

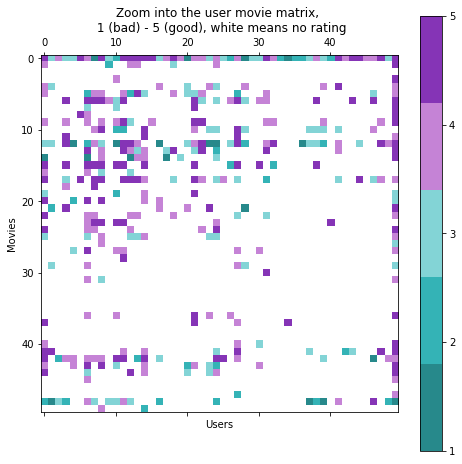
Die Bilder bestätigen die anfänglichen Beobachtungen über die Spärlichkeit dieser Matrix. Ein weiterer interessanter Aspekt ist, dass es sichtbare Korrelationen zwischen den Spalten und Zeilen der Matrix gibt. Dies macht intuitiv Sinn, da es Filme gibt, die einfach gut sind (und daher hauptsächlich gute Bewertungen erhalten) - dies erklärt die Ähnlichkeit zwischen den Zeilen. Außerdem gibt es Nutzer, die tendenziell bessere Bewertungen abgeben als andere - dies erklärt die Korrelationen zwischen den Spalten.

Im Falle des rein kollaborativen Filterns ist die Aufgabe, die wir lösen wollen, die Vorhersage, wie jeder Nutzer jeden Film bewerten würde - und damit die fehlenden Einträge in der User-Movie-Matrix.

Train Test Split

Um die Performance der Algorithmen zu bewerten, müssen wir einen Testsatz erstellen. Idealerweise sollte jeder Nutzer und jeder Film sowohl in der Trainings- als auch in der Testmenge vorhanden sein. Da es aber Filme gibt, die nur einmal bewertet wurden, ist dies nicht möglich. Daher werden wir die nur einmal bewerteten Filme aussortieren und eine Aufteilung mit der Eigenschaft erstellen, dass jeder Benutzer und jeder Film, die in der Trainingsmenge vorkommen, auch in der Testmenge vorkommen.

Leider verbleiben auf diese Weise nur 1541 Filme (von 1682) in unserem Datensatz. Für die aussortierten Filme wäre es jedoch ohnehin sehr schwierig gewesen, sinnvolle Vorhersagen zu treffen, und mit den verfügbaren Daten hätten wir diese Vorhersagen auch nicht richtig auswerten können.

Auswertung

Wie werden wir also die Vorhersagen auswerten? Beachten Sie zunächst, dass die meisten gängigen Strategien die Vorhersage von Bewertungen als Regressionsproblem formulieren - das bedeutet, dass die Ausgabe unserer Modelle eine kontinuierliche Variable sein wird, obwohl die Bewertungen diskret sind (nur im Bereich von 1-5). Typische Bewertungskennzahlen für Regressionsprobleme sind der MAE (mittlerer absoluter Fehler) und der MSE (mittlerer quadratischer Fehler) sowie der RMSE (root mean squared error). Eine weitere typische Metrik für Regressionsprobleme ist der R² - Wert, der grob gesagt beschreibt, wie viel der Varianz in den Daten durch ein Modell beschrieben wird. Seltsamerweise scheint er in Online-Ressourcen zum MovieLens100K-Datensatz nicht weit verbreitet zu sein. In diesem Blog-Beitrag werde ich mich nur auf den RMSE konzentrieren, da er die am häufigsten verwendete Metrik für diesen Datensatz ist, aber im Notizbuch gebe ich alle 3 Metriken an. Falls Sie mit dem RMSE nicht vertraut sind: Er benachteiligt größere Abweichungen von der Grundwahrheit stärker und ist bei kleinen Fehlern nachsichtiger. Im Allgemeinen kann man sagen, je niedriger diese Kennzahl ist, desto besser, und ein RMSE von 0 bedeutet eine perfekte Anpassung der Daten.

Baseline

Um unsere Ergebnisse später mit etwas vergleichen zu können, beginnen wir mit einer sehr einfachen und nicht personalisierten Basis - für jedes unbekannte Nutzer-Film-Paar sagen wir den Mittelwert aller Bewertungen voraus, die andere Nutzer diesem Film gegeben haben. Wenn wir diese Algorithmen in Empfehlungsmaschinen umwandeln, würde dies am Ende bedeuten, dass wir nur die am besten bewerteten Filme empfehlen.

Die mit diesem Ansatz erstellte Benutzer-Film-Matrix sieht ziemlich langweilig aus, da alle Zeilen gleich aufgebaut sind. Schauen wir sie uns trotzdem an, denn sie sieht irgendwie hübsch aus:

Die Auswertung unserer Testmenge ergibt folgende Kennzahlen (beachten Sie, dass wir die Mittelwerte nur auf der Trainingsmenge berechnet haben).

• RMSE: 1.022

Dieser Ansatz ist definitiv nicht der ausgeklügeltste. Wir haben keinerlei Informationen über die Benutzer berücksichtigt, so dass wir keine personalisierten Empfehlungen erwarten können. Tatsächlich ist der Rang dieser Benutzer-Film-Matrix gleich 1, da alle Spalten konstant sind!

Aus reiner Neugierde können wir das Gleiche für die Benutzer tun. Beachten Sie jedoch, dass dies aus der Sicht einer Empfehlungsmaschine nutzlos ist, da alle Filme für jeden Benutzer die gleiche Bewertung haben. Wir erhalten die folgenden Metriken:

• RMSE: 1.042

Wie wir später sehen werden, sind diese Metriken eigentlich gar nicht so schlecht. Dies verdeutlicht eine wichtige Herausforderung bei der Auswertung von Empfehlungssystemen, da beide Ansätze im Grunde nutzlos sind, wenn es darum geht, personalisierte Empfehlungen zu geben, aber dennoch anständige Ergebnisse liefern, wenn sie mit diesen Metriken bewertet werden. Der erste Ansatz wird jedoch häufig verwendet, wenn einfach keine Informationen verfügbar sind, z. B. wenn sich ein neuer Nutzer bei einem Streaming-Dienst anmeldet.

Der Algorithmus, der als Baseline von der surprise Bibliothek vorgeschlagen wird, ist etwas ausgefeilter. Er führt für jeden Benutzer und jeden Film einen (skalaren) bias ein, $$b_u$$ bzw. $$b_i$$. Diese Verzerrungen sind lernbare Parameter. Die Vorhersage ist dann definiert als

wobei $$\mu$$ der Mittelwert aller gegebenen Bewertungen in der Trainingsmenge ist. Die Parameter werden durch gradient descent auf der Trainingsmenge gelernt.

Diese Matrix sieht viel diverser aus als die beiden vorherigen und auch die Metriken sind besser. Die Korrelationen zwischen den Zeilen und Spalten sind jedoch immer noch deutlich sichtbar, was sinnvoll ist, da sie die gelernten Biases für jeden Nutzer und Artikel widerspiegeln. Man beachte auch, dass dieser Ansatz aus der Perspektive personalisierter Empfehlungen wieder "nutzlos" ist - die Rangfolge der Filme ist für jeden Nutzer immer noch die gleiche, da sie nur von den gelernten Filmvorurteilen $$b_i$$ abhängt.

Die Auswertung der Testmenge ergibt folgendes Ergebnis:

• RMSE : 0.944

Werfen wir auch einen Blick auf die Verteilung der Bewertungen. Das linke Diagramm ist ein Histogramm aller 1541*943 Vorhersagen des Basismodells, während auf der rechten Seite nur die ~100k Bewertungen zu sehen sind, für die wir tatsächliche Bewertungen haben.

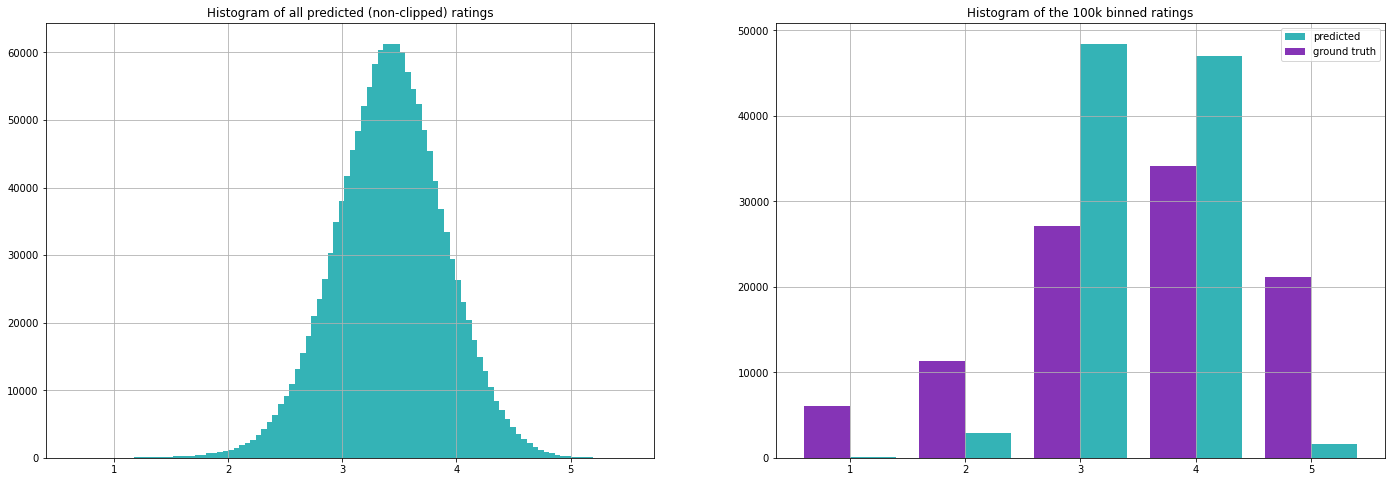
Die Verteilung auf der linken Seite sieht recht gaußförmig aus, mit einem Mittelwert, der nahe am Mittelwert aller Bewertungen im Trainingsdatensatz liegt. Allerdings ist das Modell eher zögerlich bei der Vorhersage der "extremen" Werte 1 und 5 - dies ist insbesondere in der rechten Grafik zu erkennen. Betrachtet man die Formel, so ist es sinnvoll, dass die meisten Vorhersagen sehr nahe am Mittelwert liegen und dass die Extremwerte selten sind, denn damit eine Bewertung sehr niedrig (oder hoch) ausfällt, sollte entweder der Film oder der Nutzereinfluss sehr niedrig (oder hoch) sein, was wiederum dazu führen würde, dass mehr andere Bewertungen niedrig (oder hoch) ausfallen.

Beginnen wir nun mit dem ersten "echten" Algorithmus. Ich habe mich dafür entschieden, einen Algorithmus auf der Grundlage von kNN ("k nearest neighbours") vorzustellen, da er meiner Meinung nach am intuitivsten ist und die Idee des kollaborativen Filterns auf eine sehr offensichtliche Weise widerspiegelt. Er funktioniert folgendermaßen:

Für eine gegebene Benutzer-Film-Interaktion werden die k (dies ist ein Hyperparameter dieses Algorithmus) nächsten Nachbarn des Benutzers (d.h. die ähnlichsten Benutzer) gefunden, die diesen Film ebenfalls bewertet haben. Nun berechnet man den gewichteten Durchschnitt (gewichtet nach der Ähnlichkeit der anderen Benutzer mit diesem Benutzer) der Bewertungen der gefundenen Benutzer für diesen Film - und das ist die Vorhersage. Man formalisiert den Begriff der nächsten Nachbarn oder ähnlichsten Benutzer durch Einführung eines Ähnlichkeitsmaßes $sim(u, v)$, das hoch ist, wenn die Benutzer $$u$$ und $$v$$ ähnlich sind. Ein typisches und intuitives Ähnlichkeitsmaß basiert auf dem euklidischen Abstand - Benutzer sind sich ähnlicher, wenn ihr euklidischer Abstand klein ist. Um es noch einmal in eine Formel zu fassen: Der Abstand ist gegeben durch

wobei $$I_{uv}$$ die (möglicherweise kleine) Menge der von den beiden Benutzern u und v bewerteten Elemente ist. Die Ähnlichkeit kann dann definiert werden als

wobei die 1 im Nenner vorhanden ist, um eine Division durch 0 zu vermeiden und diese Größe von oben durch 1 zu beschränken. Ein weiteres weit verbreitetes Ähnlichkeitsmaß ist die Kosinusähnlichkeit.

Da wir in unserem Fall keine weiteren Informationen über die Benutzer haben, charakterisieren wir jeden Benutzer mit dem Vektor der von ihm abgegebenen Bewertungen. Jeder Benutzer wird also mit einem Vektor $$u_i \in \mathbb{R}^{1541}$$ identifiziert, da wir 1541 Filme in unserem gefilterten Datensatz haben. Es sei daran erinnert, dass für die meisten Benutzer die meisten Einträge dieses Vektors leer sein werden. Die Suche nach den nächsten Nachbarn bedeutet also, Vektoren zu finden, die dem Vektor des gegebenen Benutzers am ähnlichsten_ sind.

Die Formel für die Vorhersage lautet

wobei $$N_i^k (u)$$ die Menge der (höchstens) $$k$$ Nachbarn von Benutzer $$u$$ ist, die den Film $$i$$ ebenfalls bewertet haben, und $$sim(u, v)$$ das oben beschriebene Ähnlichkeitsmaß ist.

Schauen wir uns also einmal an, welche Ergebnisse dieser Ansatz bringt!

• RMSE : 0.981

Hier haben wir uns entschieden, die 40 ähnlichsten Nutzer zu berücksichtigen (falls es so viele sind) und das Ähnlichkeitsmaß auf der Grundlage des oben definierten euklidischen Abstands zu wählen. Die Kosinus-Ähnlichkeit führt zu wesentlich schlechteren Ergebnissen, was sich jedoch leicht anhand des extremen Beispiels erklären bzw. veranschaulichen lässt, bei dem zwei Nutzer nur einen bewerteten Film gemeinsam haben, der eine jedoch die beste (5) und der andere die schlechteste Bewertung (1) abgab. Da die Kosinusähnlichkeit die (in diesem Fall eindimensionalen) Vektoren auf die Einheitsnorm normiert, stellen sie sich als am ähnlichsten heraus - was in diesem Fall das genaue Gegenteil von dem ist, was wir wollen! Abhilfe kann man schaffen, indem man die Bewertungen um 0 herum zentriert, z. B. indem man von allen Bewertungen 3 abzieht. Die Ergebnisse, die sich in diesem Fall ergaben, waren immer noch etwas schlechter als die berichteten (die das Ähnlichkeitsmaß auf der Grundlage des euklidischen Abstands verwenden), so dass ich sie hier nicht wiedergeben werde.

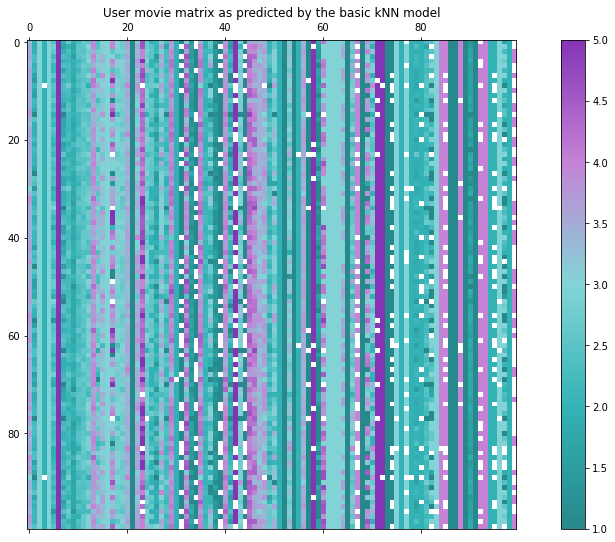
Beachten Sie, dass vor allem im rechten Teil dieser Matrix viele kleine weiße Punkte zu finden sind - insgesamt sind es 3460 Stück. Diese entsprechen Nutzer-Element-Paaren, bei denen der Algorithmus zu wenig Informationen hatte, um eine Vorhersage zu treffen. Auch wenn es also andere Nutzer gab, die diesen bestimmten Film bewertet haben, hatten sie keinen einzigen anderen Film mit diesem Nutzer gemeinsam, so dass es keine Möglichkeit gab, Ähnlichkeiten zu berechnen und der Nutzer somit keine Nachbarn in diesem Raum hatte.

Dies ist ein großer Nachteil von nachbarschaftsbasierten Algorithmen in solchen spärlichen Szenarien. Eine offensichtliche Abhilfe wäre es, in einem solchen Fall einfach den Mittelwert dieses Films oder den globalen Mittelwert aller Bewertungen vorherzusagen. Werfen wir abschließend noch einen Blick auf die Verteilung der vorhergesagten Bewertungen.

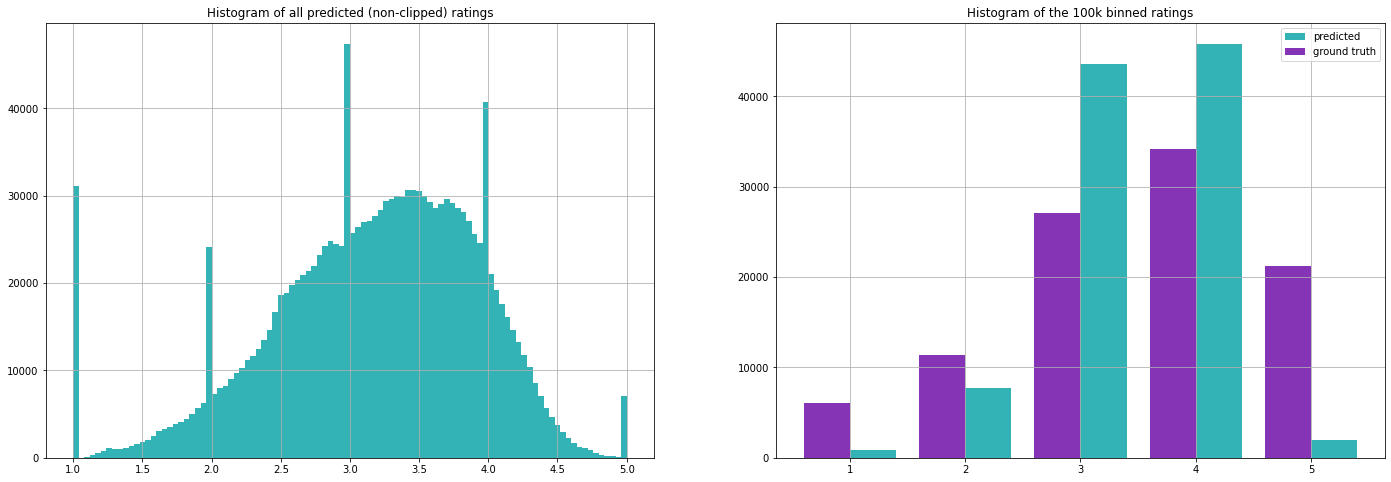
Beachten Sie die auffälligen Spitzen um die ganzen Zahlen in der linken Grafik. Sie sind ein Artefakt, das durch die geringe Anzahl der Daten und den Aufbau des Algorithmus verursacht wird. Bei vielen Nutzer-Film-Paaren gibt es nur einen Nachbarn, der diesen Film ebenfalls bewertet hat, und daher wird seine Bewertung einfach kopiert.

Um diese Schwächen des naiven kNN-Algorithmus zu beheben, kann man auch eine zugrundeliegende Baseline nehmen (z. B. die mittlere Bewertung) und ein kNN-Modell trainieren, um diese Baseline zu verbessern. Die Formel lautet dann

wobei $$b_{ui}$$ die Basisvorhersage ist, die sowohl vom Benutzer als auch vom Film abhängen kann, aber nicht muss. Wählt man die Baseline als mittlere Bewertung der gesamten Trainingsmenge, d.h. $$b_{ui} = \mu$$, erhält man die folgenden Metriken und Bilder:

• RMSE : 0.954

Beachten Sie, dass sich das Intervall, in dem die Vorhersagen liegen, plötzlich drastisch vergrößert hat und das Modell Werte von 7 bis -1 ausgibt. Das liegt daran, dass die Formel jetzt eine weitere Addition beinhaltet und nicht nur den Durchschnitt der bereits vorhandenen Werte nimmt, wie es unsere früheren Algorithmen taten. Wir können dies leicht beheben, indem wir die Werte bei 1 und 5 abschneiden.

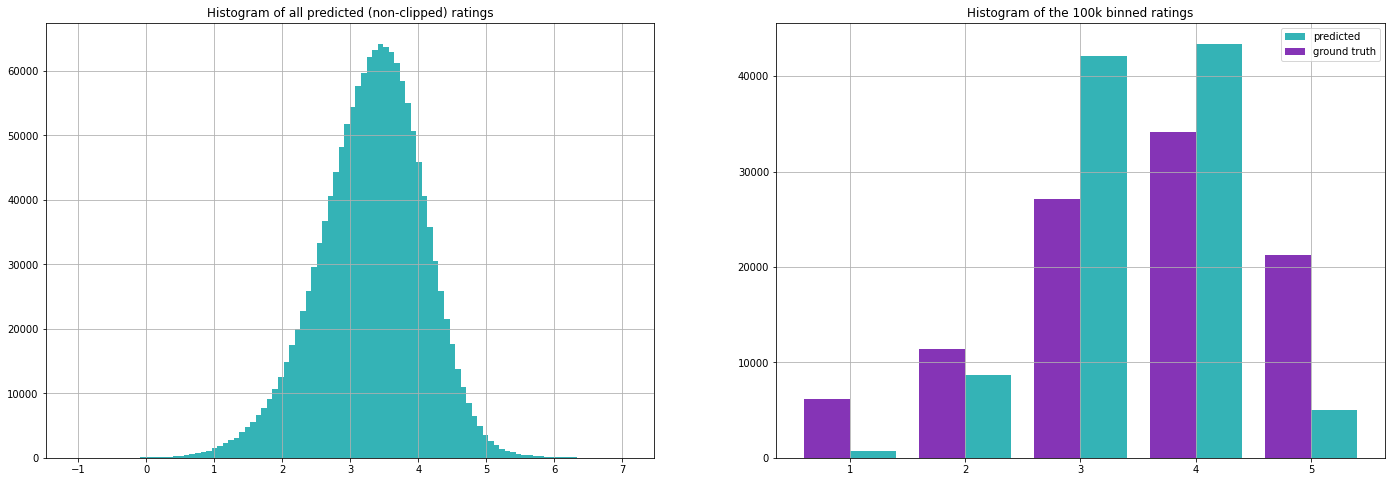
Insgesamt hat diese Variante:

• unsere Bewertungsmetriken besser gemacht

• eine diversere Nutzer-Film-Matrix erzeugt

• das Problem, keine Vorhersage treffen zu können, wurde beseitigt (da der Mittelwert in diesem Fall die Standardvorhersage ist)

Die Verwendung der oben definierten Baseline als Baselinie für den kNN-Algorithmus verbessert die Metriken noch weiter:

• RMSE : 0.934

Da die Bilder, die diesem Ansatz entsprechen, dem vorherigen sehr ähnlich sind, werde ich sie hier nicht zeigen.

Betrachten wir nun eine andere Familie erfolgreicher Algorithmen für die kollaborative Filterung - jene, die auf Matrixfaktorisierung basieren.

Wir haben bereits festgestellt, dass die Spalten und Zeilen in der User-Movie-Matrix $$M$$ wahrscheinlich korreliert sind. Mathematisch ausgedrückt bedeutet dies, dass diese Matrix wahrscheinlich nicht vollen Rang hat. Algorithmen, die auf Matrixfaktorisierung beruhen, nutzen diese Tatsache aus, indem sie diese Matrix als Produkt $$A \in \mathbb{R}^{943 \times k}$$ und $$B \in \mathbb{R}^{k \times 1541}$$ so faktorisieren, dass $$M \approx AB$$.

$$k$$ ist hier ein freier Parameter und wird typischerweise viel kleiner als die Dimensionen der User-Movie-Matrix gewählt. Konstruktionsbedingt wird der Rang der faktorisierten Matrix höchstens $$k$$ betragen.

Ein weiterer Vorteil dieses Ansatzes ist, dass er ganz natürlich zum Begriff von Einbettungen führt - ein sehr grundlegendes Konzept in der Data Science und im maschinellen Lernen.

Die Matrizen $$A$$ und $$B$$ können als Sammlungen von Vektoren der Länge $$k$$ verstanden werden - Einbettungen der Benutzer und Elemente in einem gemeinsamen Vektorraum $$\mathbb{R}^k$$. Konstruktionsbedingt wird die Interaktion zwischen Benutzer $$i$$ und Gegenstand $$j$$ dann als das Skalarproduktprodukt ihrer jeweiligen Einbettungsvektoren modelliert - es gilt $$M_{ij} = A_i \cdot B_j$$.

In der Literatur und der Überraschungsbibliothek wird dieser Ansatz unter dem Namen SVD (Singulärwertzerlegung) geführt, da er auf diesem Konzept aus der linearen Algebra beruht. Probieren wir es aus!

SVD-Algorithmus

• RMSE : 0.944

Werfen wir noch einmal einen Blick auf die vollständige Benutzer-Filmmatrix. Beachten Sie, dass die Vorhersagen wieder außerhalb des Bereichs [1, 5] liegen können, also schneiden wir sie entsprechend ab.

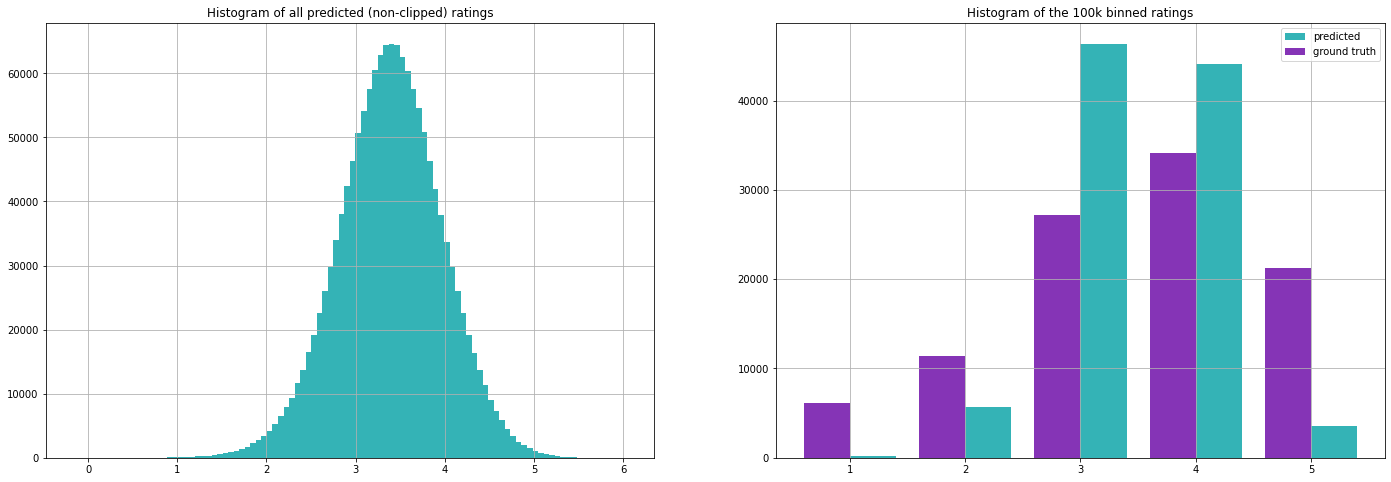
Beachten Sie, dass es in unseren Vorhersagen Filme gibt, die von verschiedenen Nutzern gleich gut bewertet werden, sowie einige Nutzer, die über verschiedene Filme hinweg gleich gute (oder schlechte) Bewertungen abgeben. Dieses Muster konnten wir auch in dem Trainingsset beobachten und es ergibt auch Sinn, dass manche Filme einfach gut sind und manche Leute einfach alle Arten von Filmen mögen :)

Einfluss der EInbettungsdimension

In unserer Matrixfaktorisierung haben wir k = 100 gewählt, so dass wir davon ausgehen, dass die Nutzer-Film-Matrix (höchstens) einen Rang von 100 hat. Ein niedrigerer Rang bedeutet, dass die Zeilen und Spalten stärker korreliert sind, d. h. dass es weniger Varianz zwischen den Bewertungen der Nutzer bzw. der Filme gibt. Schauen wir uns an, wie unsere Metriken abschneiden, wenn wir verschiedene Werte für k wählen.

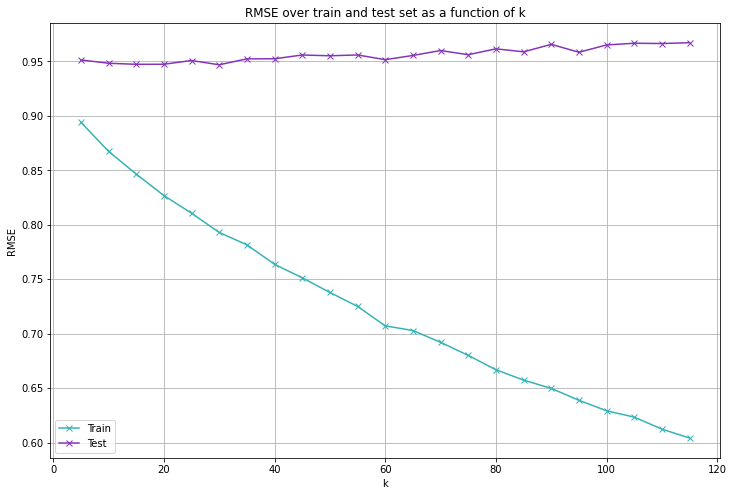
Indem wir ein größeres $$k$$ wählen, machen wir den Algorithmus leistungsfähiger, so dass er einen geringeren RMSE auf der Trainingsmenge erzielen kann. Der Fehler auf der Testmenge wird davon jedoch kaum beeinflusst - er ist für $$k = 30$$ am niedrigsten und bereits $$k = 15$$ erzeugt vernünftige Ergebnisse. Es sieht also so aus, als ob die Wahl von $$k = 100$$ viel zu groß war.

Eine erneute Ausführung des Algorithmus mit $$k = 30$$ liefert folgende Ergebnisse:

• RMSE : 0.951

Die Bilder und die Verteilung der Bewertungen sind dem Fall mit der größeren Einbettungsdimension sehr ähnlich, so dass ich sie hier nicht zeigen werde.

Der Algorithmus, den wir jetzt verwenden, entspricht einer Technik, die als probabilistische Matrixfaktorisierung bekannt ist. Wir faktorisieren einfach (stochastisch) die User-Movie-Matrix und nehmen die Einträge der resultierenden Matrix als Vorhersagen. Die surprise Bibliothek bietet auch Varianten des SVD-Algorithmus, der versucht, ein bestehendes Basismodell zu verbessern. Da die Ergebnisse jedoch nicht wesentlich besser waren, werde ich sie nicht in diesen ohnehin schon recht langen Blogpost aufnehmen.

Deep Learning

Es ist natürlich auch möglich, Empfehlungssysteme mit Deep Learning anzugehen. Im Kontext der kollaborativen Filterung und insbesondere bei einem so kleinen Datensatz erweist sich dies jedoch als nicht sehr effektiv. Im nächsten Artikel, in dem wir uns mit inhaltsbasierter Filterung befassen, werden wir viele interessante Deep-Learning-Algorithmen in Betracht ziehen.

Ich möchte kurz veranschaulichen, wie wir nun einen der betrachteten Algorithmen in ein tatsächliches Empfehlungssystem verwandeln würden.

In dieser rein kollaborativen Umgebung, in der wir keine weiteren Informationen über die Nutzer und die Artikel haben, wird dies wahrscheinlich nicht allzu aufschlussreich sein, aber es ist dennoch ein notwendiger Baustein.

Wir müssen 2 Dinge tun:

• für einen bestimmten Benutzer die Filme herausfiltern, die er bereits bewertet hat;

• die vorhergesagten Bewertungen absteigend sortieren und die besten n (sagen wir n = 5) Filme zurückgeben.

Angenommen, wir haben ein Modell, das auch alle Interaktionen aus dem Trainingssatz enthält, und wir können die Vorhersage aus einem Modell für ein bestimmtes Benutzer-Element-Paar mit der Methode get_estimate extrahieren, dann könnte der Code für eine Klasse, die dies tut, wie folgt aussehen (schauen Sie sich das verlinkte Notebook für den tatsächlichen Code an):

Wir können nun eine Stichprobe von zufällig ausgewählten Nutzern durchführen und ihre 5 besten Empfehlungen betrachten.

Recommended movies for user 792:
[603 233 296  52 643]
Recommended movies for user 846:
[603 233 296 512  52]
Recommended movies for user 498:
[512  52 437 296 233]

Einige Filme tauchen in allen 3 ausgewählten Empfehlungen auf, andere in 2 von ihnen. Dies könnte ein Zufall sein, aberprüfen wir, wie sie in der Trainingsmenge bewertet werden.

Es scheint sich also nur um beliebte Filme zu handeln, die von einigen Personen bewertet wurden. Die durchschnittliche Bewertung von Film 233 ist nicht allzu hoch, aber ein Blick auf das Histogramm unten zeigt, dass er in der Trainingsgruppe im Allgemeinen gut bewertet wird.

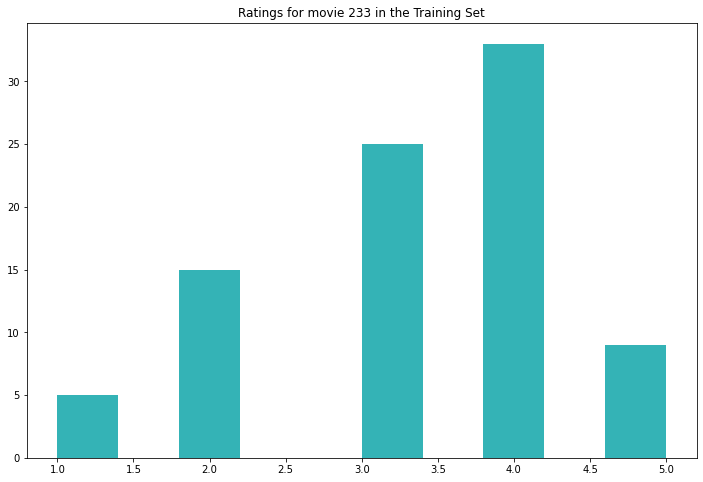
Um ein Gefühl dafür zu bekommen, wie vielfältig die Empfehlungen sind, können wir die Top-5-Empfehlungen für jeden Nutzer berechnen und sie analysieren. Insgesamt gibt es nur 72 Filme (von den 1541 Filmen insgesamt), die empfohlen werden. Untersuchen wir nun, wie oft jeder dieser Filme in den Top-5-Empfehlungen eines Nutzers vorkommt.

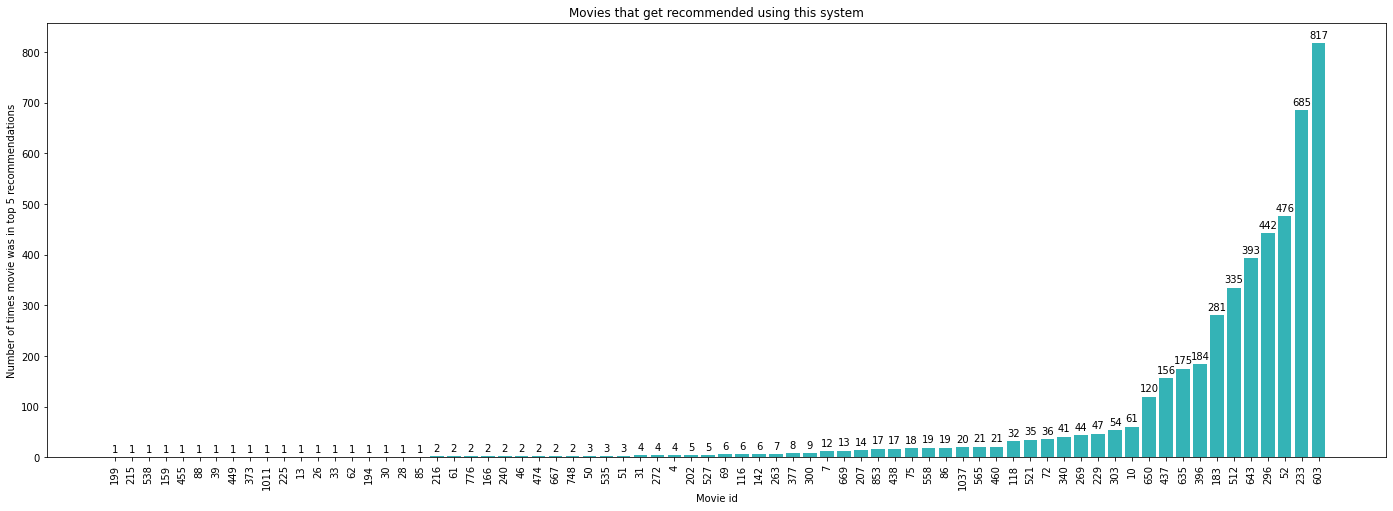
Offensichtlich empfiehlt unser Empfehlungssystem also fast jedem Nutzer die Filme mit den IDs 233 und 603. Da es sich dabei wahrscheinlich um sehr beliebte Filme handelt, macht das auch Sinn.

Was schön ist, ist, dass es auch einige Filme gibt, die zwischen 10-50 Mal empfohlen werden. Was ich auch interessant finde, sind die Filme, die nur ein oder zwei Mal empfohlen werden. Es wäre wirklich interessant zu untersuchen, ob sie "Sinn" ergeben, d.h. ob sie in gewisser Weise den Filmen ähneln, die ein bestimmter Nutzer gut bewertet hat. Da wir aber keine Informationen über die Filme verwenden, ist dies im Moment nicht möglich.

Bisher haben wir das Problem als Regressionsproblem formuliert. Auch die von uns zur Bewertung verwendeten Metriken sind in einem Regressionsszenario sehr üblich. Dies ist aus mindestens 2 Gründen sehr sinnvoll:

* Die vorhergesagte Variable hat eine klare Interpretation. Eine höhere Bewertung bedeutet einfach, dass der Nutzer den Film mit größerer Wahrscheinlichkeit mögen wird.

* Wenn man diese Algorithmen in tatsächliche Empfehlungsmaschinen umwandelt, kommen die Empfehlungen auf natürliche Weise mit einem Ranking - es kann sogar Elemente geben, die höher bewertet werden als die eigentlich mögliche Maximalbewertung, wie wir gesehen haben.

Dennoch ist es interessant, die Leistung auf unserer Testmenge zu bewerten, als ob es sich um ein Klassifizierungsproblem handeln würde. Wir runden die Vorhersagen einfach auf die nächste natürliche Zahl und werfen dann einen Blick auf die Confusion Matrix.

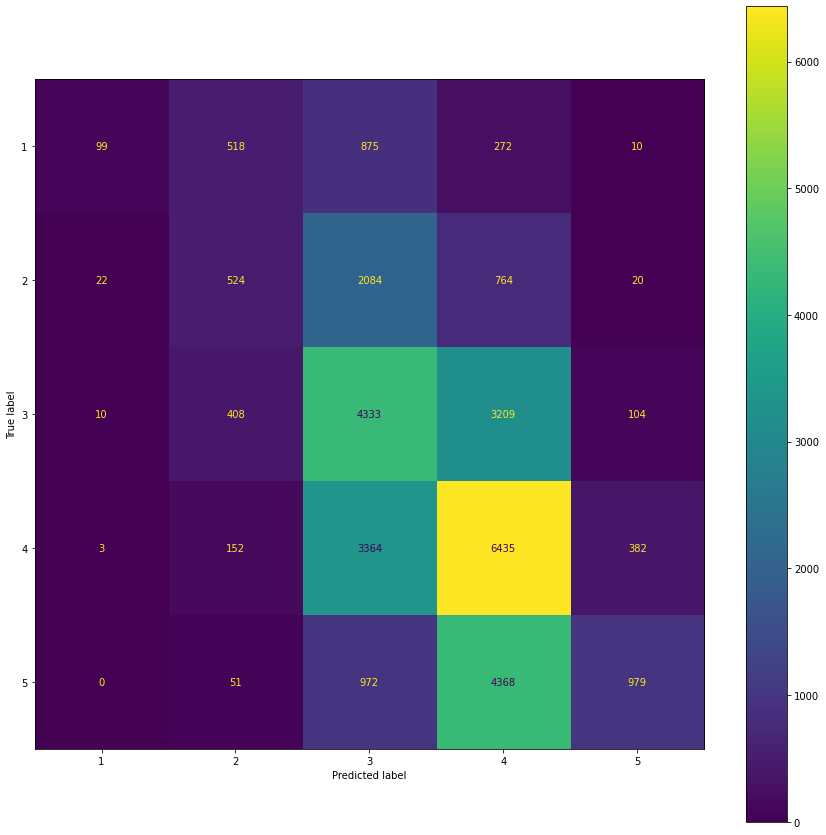
Aus dieser Confusion Matrix lassen sich einige interessante Dinge ablesen. Erstens hat unser Modell alle Arten von Fehlern auf der Testmenge gemacht, mit Ausnahme der Vorhersage einer 1, wenn die tatsächliche Bezeichnung eine 5 war. Das ist eine recht gute Nachricht, da dies die schlimmste Art von Fehler ist (zusammen mit der Vorhersage einer 5, wenn die Grundwahrheit eine 1 war, was 10 Mal vorkam). Die häufigste Fehlerart sind Verwechslungen zwischen 3 und 4 bzw. 4 und 5. Diese Fehler sind nicht so schlimm, da sie immer noch die allgemeinen Präferenzen widerspiegeln.

Bevor wir diesen Artikel abschließen, wollen wir die verschiedenen betrachteten Algorithmen im Hinblick auf den RMSE (Root Mean Square Error) vergleichen.

Was ich besonders interessant finde, ist, dass das Basismodell mit nur einem lernbaren Parameter pro Nutzer und Film (also 943 + 1541 = 2484 Parameter insgesamt) tatsächlich besser ist als einige der kNN-basierten Methoden und auch sehr nahe an der Leistung des tatsächlich "besten" Modells liegt. Dieses "beste" Modell (von den Modellen, die wir für diesen speziellen Testsatz in Betracht gezogen haben) ist das kNN-basierte Modell, das darauf abzielt, die Grundlinie zu verbessern. Ich schreibe hier "bestes Modell" in Anführungszeichen, weil es sehr schwierig ist, den Erfolg eines Empfehlungssystems mit einer Offline-Metrik zu messen. Offline bedeutet in diesem Fall, dass die Bewertung auf historischen Daten und nicht in einer Live-Umgebung durchgeführt wird.

In der Regel handelt es sich bei Empfehlungssystemen in der Produktion um hybride Modelle, d. h. sie sind ein Ensemble aus vielen verschiedenen Modellen. Um verschiedene Ensembles zu vergleichen, verwenden Unternehmen A/B-Tests: In einer Live-Einstellung erhalten einige Nutzer Version A und einige Version B. Durch den Vergleich bestimmter Geschäftskennzahlen wie Klickraten oder Konversionen kann gemessen werden, welches System besser ist.

Fassen wir also zum Abschluss dieses Blogposts die wichtigsten Punkte zusammen.

Wir haben

• das Konzept des kollaborativen Filterns vorgestellt,

• einige rein kollaborative Ansätze anhand des MovieLens100k-Datensatzes untersucht, insbesondere:

  • ein Basismodell,

  • einige auf k-nearest neighbour (kNN) basierende Modelle,

  • einen Algorithmus, der auf Matrixfaktorisierung basiert,

• einen dieser Algorithmen in ein echtes Empfehlungssystem umgewandelt und dessen Empfehlungen untersucht,

• die verschiedenen Modelle im Bezug auf einige Offline-Metriken verglichen

• und erörterte, dass die Bewertung von Empfehlungssystemen eine heikle Angelegenheit ist.

Ich hoffe, dieser Blogpost hat Ihnen einen Einblick in das Innenleben von Algorithmen der kollaborativen Filterung gegeben. Im nächsten Artikel werden wir das Konzept des inhaltsbasierten Filterns untersuchen. Vielen Dank fürs Lesen!