From Discrete-Time Policies to Continuous-Time Diffusion Samplers: Asymptotic Equivalences and Faster Training

---

arXiv preprint arXiv:2501.06148

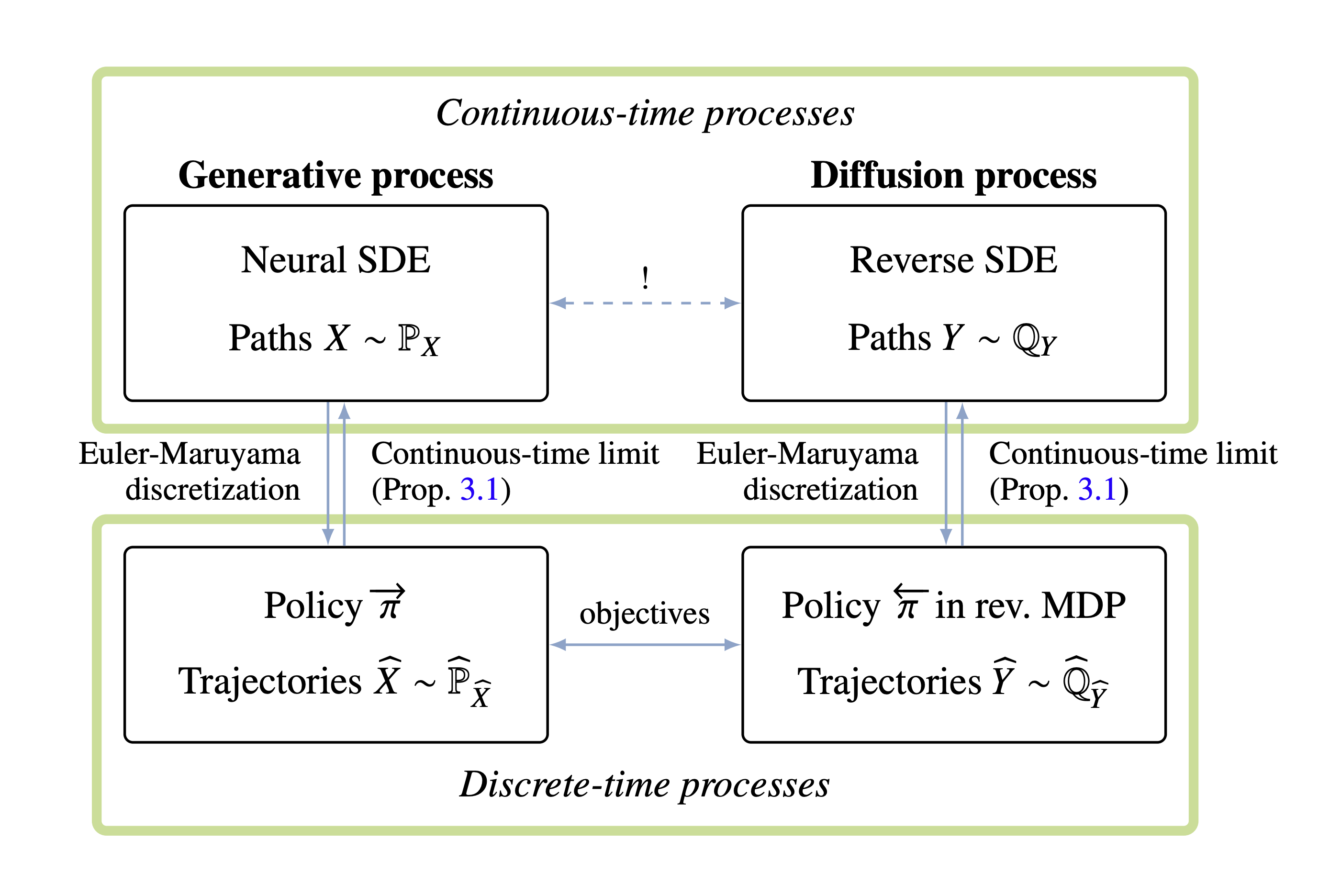
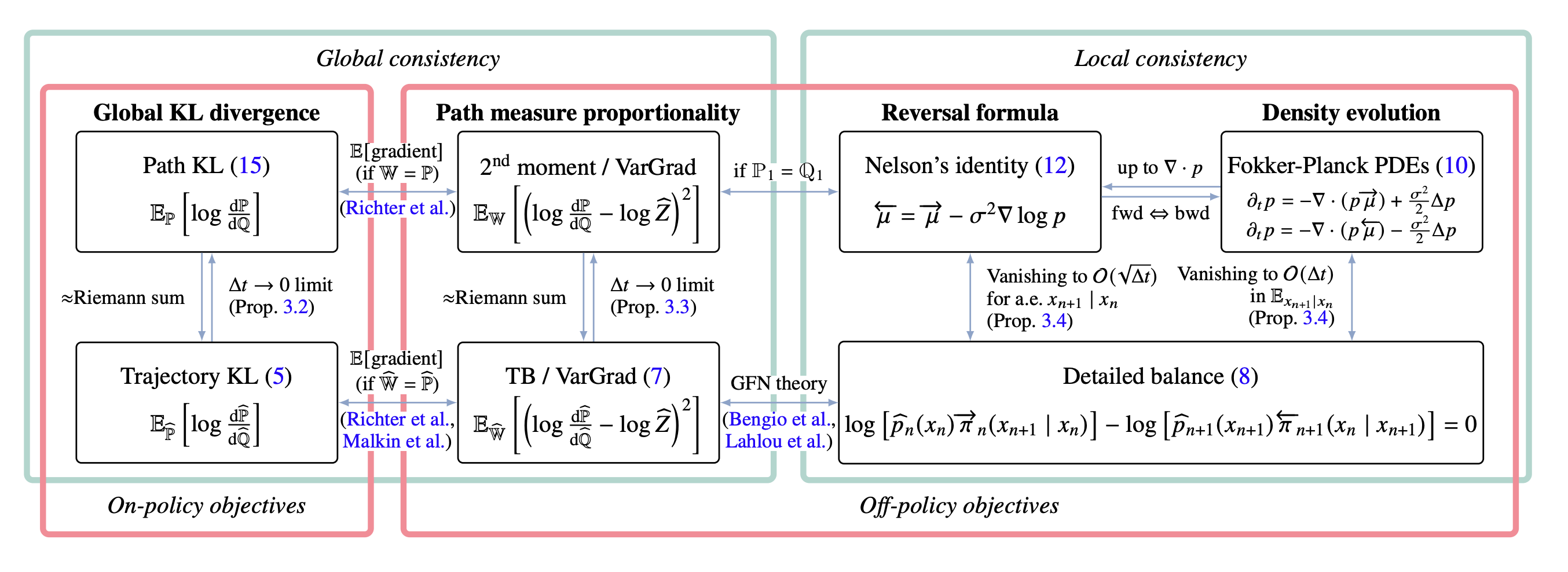
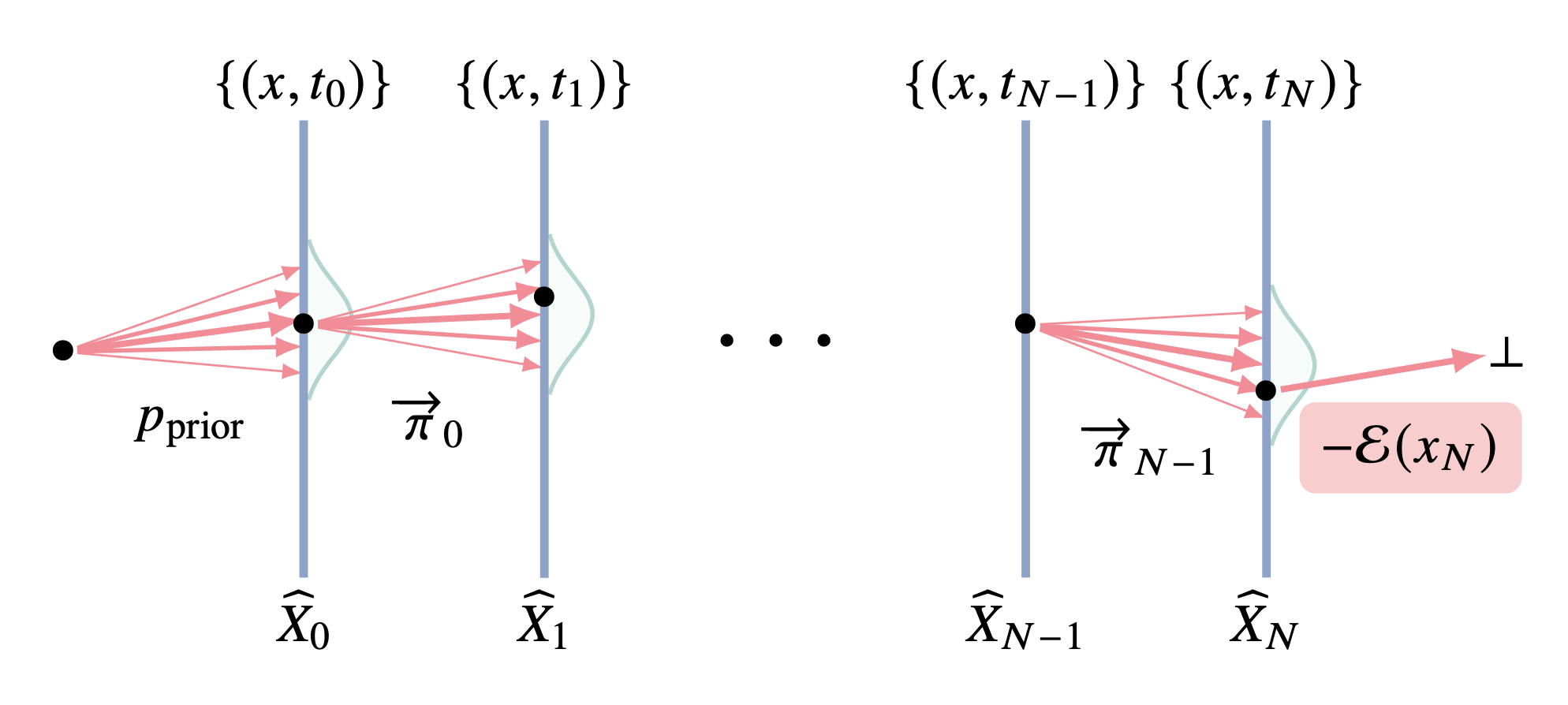
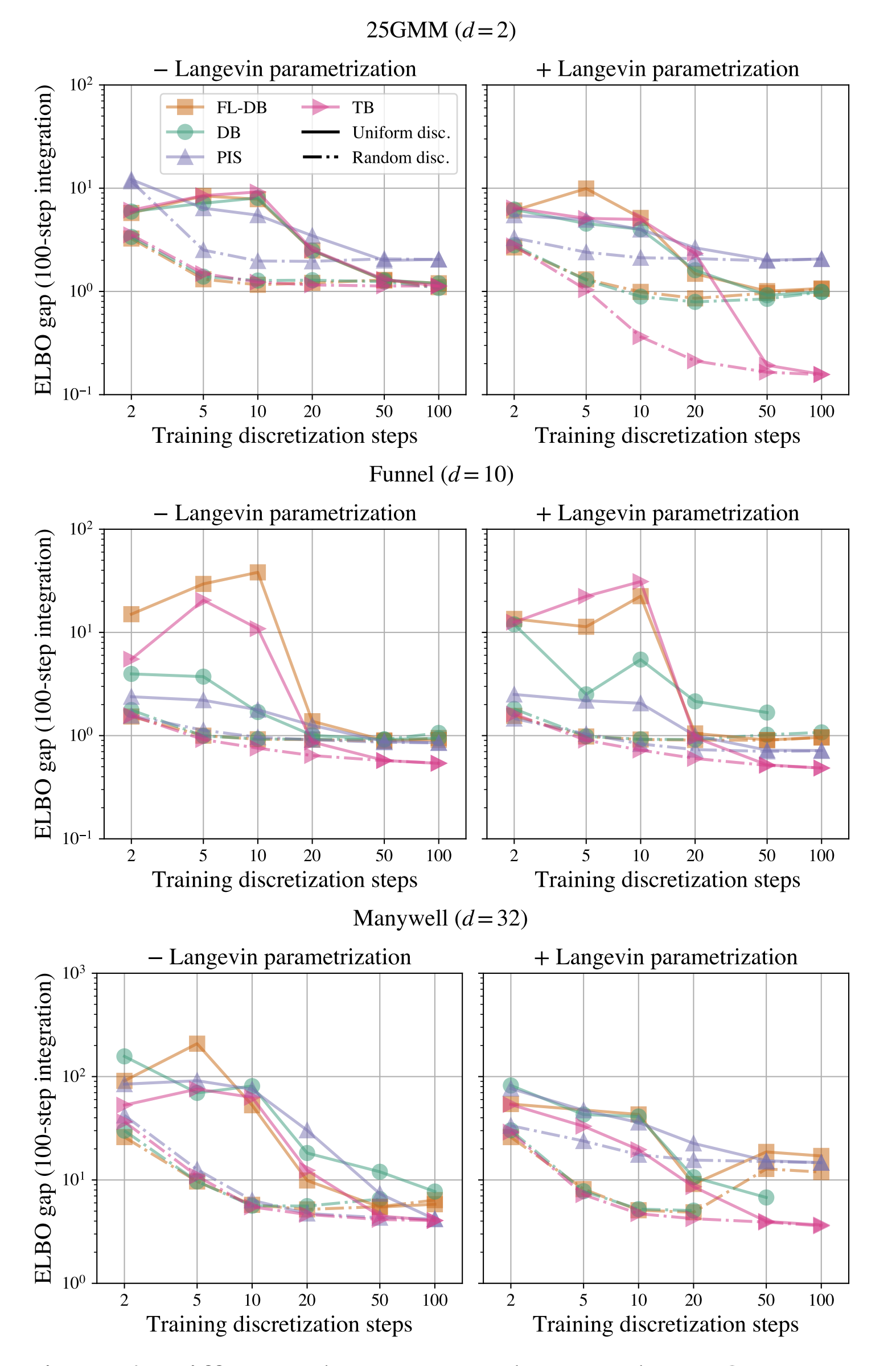
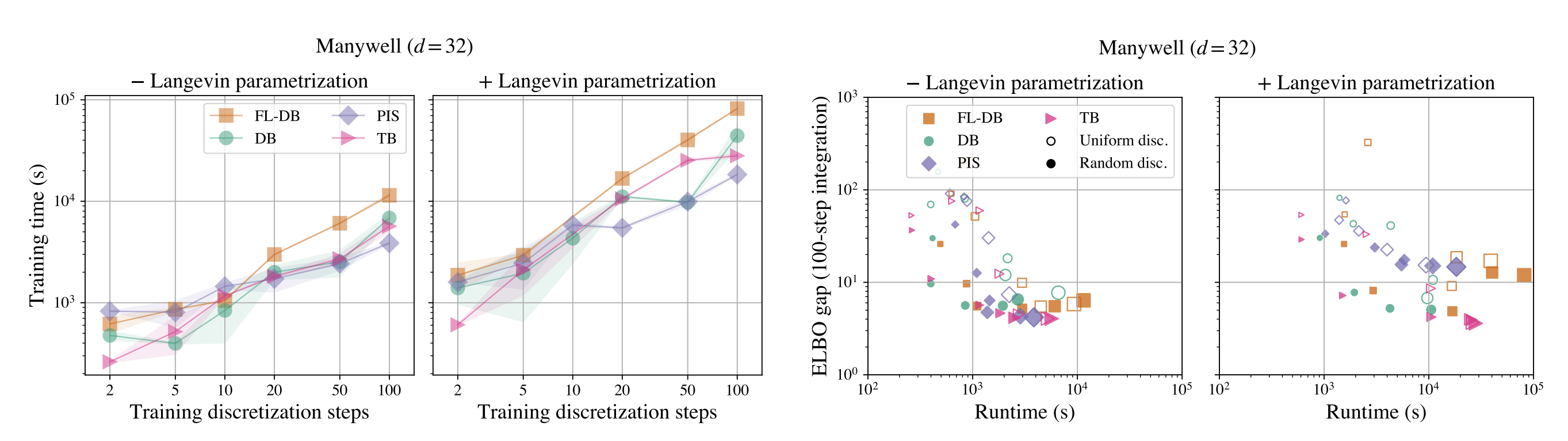
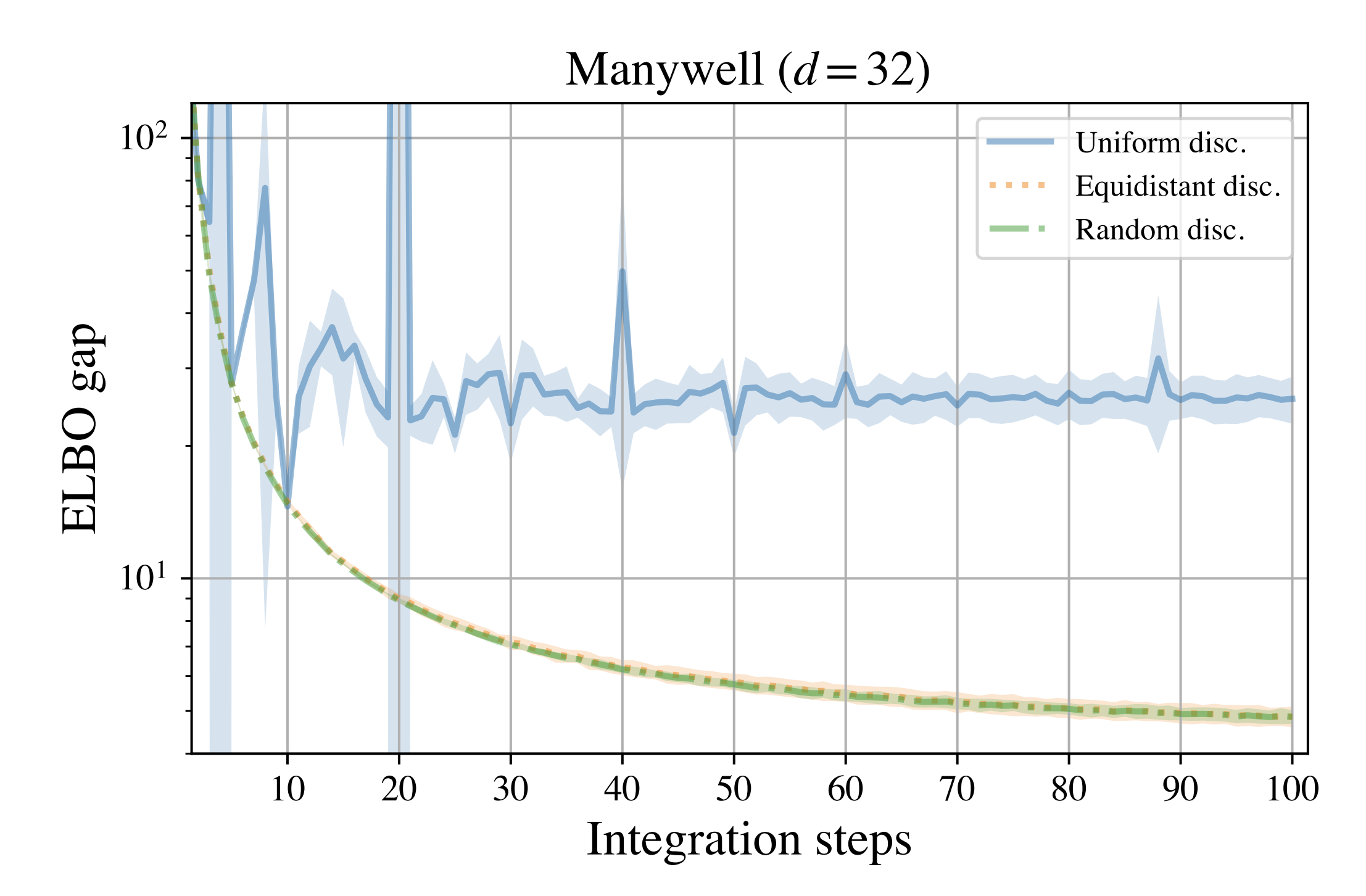
We study the problem of training neural stochastic differential equations, or diffusion models, to sample from a Boltzmann distribution without access to target samples. Existing methods for training such models enforce time-reversal of the generative and noising processes, using either differentiable simulation or off-policy reinforcement learning (RL). We prove equivalences between families of objectives in the limit of infinitesimal discretization steps, linking entropic RL methods (GFlowNets) with continuous-time objects (partial differential equations and path space measures). We further show that an appropriate choice of coarse time discretization during training allows greatly improved sample efficiency and the use of time-local objectives, achieving competitive performance on standard sampling benchmarks with reduced computational cost.