Wozu gelabelte Daten? (Un)überwachtes Machine Learning

Lorenzo Melchior

14. April 2020

Es scheint ein weit verbreiteter Irrtum zu sein zu glauben, dass maschinelles Lernen in der Regel eine unüberwachte Aufgabe ist: Sie haben Daten (ohne vorher existierende Etiketten), die Sie z.B. in einem neuronalen Netz für Aufgaben wie Klassifikation oder Bildsegmentierung trainieren. Die Wahrheit ist, dass die meisten Modelle beim maschinellen Lernen überwacht sind, d.h. sie stützen sich auf gelabelte Trainingsdaten.

Aber das Labeling nimmt oft viel Zeit in Anspruch und kann sehr mühsam sein.

In diesem Blogbeitrag möchte ich herausfinden, ob ich in der Lage bin, die gleiche Klassifizierungsaufgabe einmal mit und einmal ohne Labels durchzuführen.

Für diese Aufgabe werde ich den bekannten MNIST-Datensatz verwenden, der 60.000 Trainings- und 10.000 Validierungsbilder handgeschriebener Ziffern enthält, die alle gelabelt sind. Jedes Bild besteht aus 28x28 Graustufenpixeln und enthält nur eine Ziffer, die sich in der Mitte des Bildes befindet. Um die Sache zu vereinfachen, verwende ich die CSV-Version des Datensatzes.

Unüberwachtes Lernen zur Klassifizierung verwenden

Wenn Sie ein Modell zum Klassifizieren von Daten trainieren möchten, verwenden Sie normalerweise Labels, die für jede einzelne Datenprobe angeben, zu welcher Klasse sie gehört, so dass Sie die typischen Muster für jede Klasse lernen können. Wenn wir nun einen Klassifikator trainieren wollen, ohne über Labels zu verfügen, müssen wir zunächst einen Weg finden, die Trainingsdatenpunkte in diese Klassen zu gruppieren. Dazu werde ich einen Clustering-Algorithmus verwenden. Er gruppiert alle Trainingsdaten, die wir haben, auf der Grundlage der Ähnlichkeit der gefundenen Daten in zehn Cluster. Man würde erwarten, dass diese Cluster den "echten" Klassen entsprechen, die den Ziffern 0-9 entsprechen.

Ich werde den k-Mittelwert-Algorithmus verwenden, der sehr einfach und intuitiv ist. Er vergleicht einfach den euklidischen Abstand zwischen allen Datenpunkten im [28x28 Pixel]-Raum (dies ist nur die Verallgemeinerung der Art und Weise, wie wir Abstände im dreidimensionalen Raum messen) und gruppiert sie entsprechend ihrer Lage in zehn Cluster. Die Intuition hinter dem Algorithmus ist, dass, wenn zwei Datenpunkte in Bezug auf den euklidischen Abstand nahe beieinander liegen, sie wahrscheinlich zur selben Klasse gehören.

Zuerst laden wir einige Abhängigkeiten:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tqdm import tqdm, tqdm_notebook


mnist_train = np.array(pd.read_csv('data/mnist_train.csv', header=None))
mnist_test = np.array(pd.read_csv('data/mnist_test.csv', header=None))

X_train = mnist_train.T[1:].T
y_train = mnist_train.T[0].T.astype(np.int32)
X_val = mnist_test.T[1:].T
y_val = mnist_test.T[0].T.astype(np.int32)

Dann definieren wir die Train- und Validierungsdatensätze:

mnist_train = np.array(pd.read_csv('data/mnist_train.csv', header=None))
mnist_test = np.array(pd.read_csv('data/mnist_test.csv', header=None))

X_train = mnist_train.T[1:].T
y_train = mnist_train.T[0].T.astype(np.int32)
X_val = mnist_test.T[1:].T
y_val = mnist_test.T[0].T.astype(np.int32)

Als nächstes richten wir den Clustering-Algorithmus ein und trainieren ihn:

from sklearn.cluster import KMeans


kmeans = KMeans(n_clusters=10, init='random', n_init=64, max_iter=1000000, n_jobs=64)
kmeans.fit(X_train)

Wir haben jetzt diese zehn Cluster gefunden. Lassen Sie uns die nächstgelegenen Schwerpunkte für die Bilder im Validierungssatz berechnen:

def euklidean_distance(a, b):
    return np.sqrt(((a - b) ** 2).sum())
    
    
groups = [[] for _ in range(10)]

for index, y in enumerate(X_val):
    distances = [euklidean_distance(y, centroid) for centroid in kmeans.cluster_centers_]
    groups[np.argmin(distances)].append(index)

Schließlich können wir uns Beispiele aus allen zehn Clustern ansehen: Wir sehen neun Zufallsstichproben für jeden Cluster, und rechts davon den berechneten Cluster-Schwerpunkt.

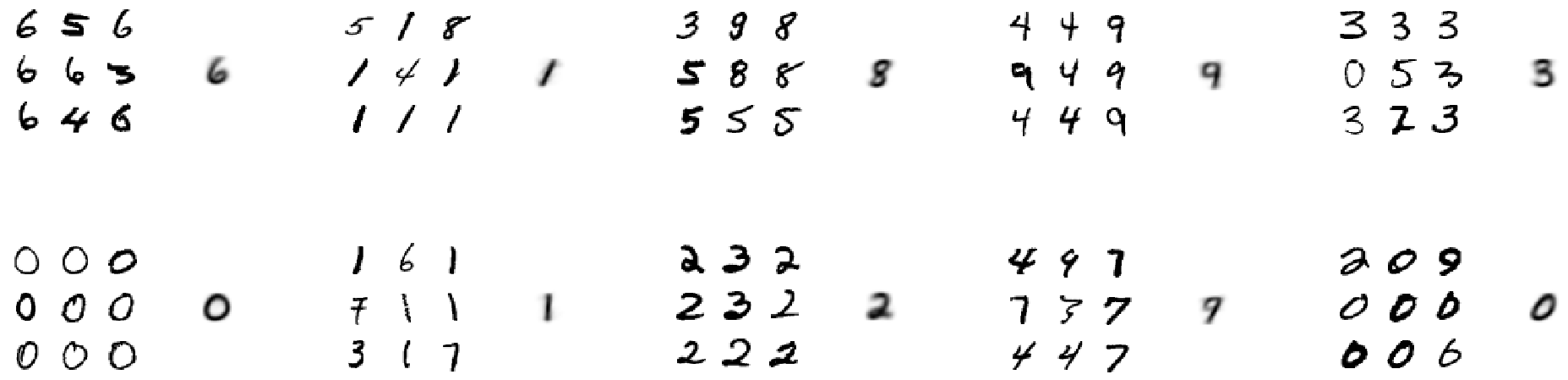
Wenn wir die Cluster untersuchen, stellen wir fest, dass sie in etwa den Klassen 6, 1, 8, 9, 3, 0, 1, 2, 9, 0 entsprechen. Anstatt also z.B. Ziffern der Klasse 5 zu clustern, unterscheidet der Algorithmus eher zwischen zwei verschiedenen Arten von 0 (dünne runde und dicke krumme, wie es scheint).

Um genauer zu analysieren, welche Klasse am besten zu welchem Cluster passt, werde ich einfach jede der 10! (= 3.628.800) möglichen Permutationen der Klassenzuweisungen ausprobieren. Beachten Sie, dass ich die Performance mit dem Validierungssatz und seinen Labels validieren werde. Wenn Sie dies wirklich komplett ohne Labels trainieren würden, würden Sie versuchen, einen anderen Weg zu finden, um zu sehen, welcher Cluster zu welcher Ziffer gehört.

from itertools import permutations
from multiprocessing import Pool


indices = []

for X in X_val:
    distances = np.array([euklidean_distance(X, centroid) for centroid in kmeans.cluster_centers_])
    indices.append(np.argmin(distances))
    
    
def validate(permutation):
    correct_predictions = 0
    for index, y in zip(indices, y_val):
        if y == permutation[index]:
            correct_predictions += 1
    return correct_predictions / len(y_val)
    

def search_for_best_permutation(permutations):
    best_permutation = None
    highest_accuracy = 0
    for index, p in enumerate(permutations):
        accuracy = validate(p)
        if accuracy > highest_accuracy:
            best_permutation = p
            highest_accuracy = accuracy
    return highest_accuracy, best_permutation
  

permutations = list(permutations(range(10)))

slices = np.array(range(17))*(int(len(permutations)/16))
p = []
for index, item in enumerate(slices):
    try:
        p += [permutations[item:slices[index+1]]]
    except:
        pass
        
with Pool(16) as pool:
    results = pool.map(search_for_best_permutation, p)

best_permutation = None
highest_accuracy = 0

for accuracy, permutation in results:
    if accuracy > highest_accuracy:
        best_permutation = permutation
        highest_accuracy = accuracy

Wir erhalten die folgende beste Permutation:

Best permutation: (5, 1, 8, 4, 2, 3, 7, 6, 9, 0)

Accuracy: 0.5173

Offensichtlich ist ein Modell, bei dem nur jede zweite Prognose richtig ist, nicht sehr leistungsfähig. Natürlich gibt es Möglichkeiten, unsere Ergebnisse zu verbessern. Ich habe k-means wegen seiner Einfachheit gewählt. Die Verwendung ausgefeilterer Algorithmen zum Auffinden der Schwerpunkte wie Erwartungsmaximierung oder DBSCAN könnte zu besseren Ergebnissen führen.

Lassen Sie uns nun sehen, ob wir durch die Verwendung der Labels bessere Ergebnisse erzielen können. Für den Ansatz des überwachten Lernens werde ich den Algorithmus k-nearest neighbors verwenden. Er ist k-means recht ähnlich, aber anstatt eine Klasse über den nächstgelegenen Schwerpunkt zuzuweisen, findet er die k nächstgelegenen gelabelten Proben in unserem 28x28-Pixel-Bildraum (wiederum unter Verwendung des euklidischen Abstands). Basierend auf den Labels der k nächstgelegenen Nachbarn entscheiden wir, zu welcher Klasse eine bestimmte Testprobe gehört. Da wir nun nach sehr wenigen, aber sehr ähnlichen Bildern suchen, sollten die Ergebnisse viel besser sein als der Vergleich mit den Durchschnittsbildern jedes Clusters.

Hinweis: Der Parameter k bestimmt, wie viele Trainingsproben wir verwenden, um zu entscheiden, zu welcher Klasse eine Testprobe gehört. Ich würde die Verwendung eines k wie 1, 3 oder 5 empfehlen.

from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix


knn = KNeighborsClassifier(n_neighbors=3, n_jobs=64)
knn.fit(X_train, y_train)

y_pred = knn.predict(X_val)

sum([confusion_matrix(y_val, y_pred)[x][x] for x in range(10)])/confusion_matrix(y_val, y_pred).sum()

Das ergibt 0.9705.

Mit nur 4 Zeilen Code sind wir in der Lage, das Modell zu generieren und zu validieren und eine Genauigkeit von 97,05% zu erreichen.

Wie viele Daten benötigen wir tatsächlich?

Da es nicht wirklich funktioniert hat, die Daten nicht zu labeln, werden wir sehen, ob wir die Datenmenge einfach reduzieren können, so dass wir nicht so viel Zeit mit dem Labeling verbringen müssen.

Hierfür werde ich den sehr leistungsfähigen und einfach zu bedienenden XGBoost-Klassifikator verwenden. Ich werde ihn mit verschiedenen Datenmengen trainieren, um herauszufinden, wie sich die Menge der Trainingsdaten auf die Leistung auswirkt.

Gleichzeitig werde ich dafür sorgen, dass der Klassifikator genügend Zeit erhält, um mit den Daten in jeder Runde so viel wie möglich zu lernen: Ich werde den Klassifikator so lange laufen lassen, bis er sich 100 Epochen lang nicht mehr verbessert hat.

Wenn Sie möchten, sehen Sie sich den Code an oder überspringen Sie ihn, um direkt zu den Ergebnissen zu gelangen.

import os
import xgboost as xgb

seed = 42
np.random.seed(seed=seed)

def generate_path():
    path = 'results/'
    tries = list(filter(lambda folder : 'try' in folder, os.listdir(path)))
    next_try = max([int(t[3:]) for t in tries]) + 1
    path += f'try{str(next_try)}'
    os.mkdir(path)
    return path

def training(number_of_training_samples=len(X_train)):
    training_data = xgb.DMatrix(data=X_train[:number_of_training_samples], 
                                label=y_train[:number_of_training_samples])
    validation_data = xgb.DMatrix(data=X_val,
                                 label=y_val)
    parameters = [("eta", 0.08), 
                  ("max_depth", 10), 
                  ("subsample", 0.8), 
                  ("colsample_bytree", 0.8), 
                  ("objective", "multi:softmax"), 
                  ("eval_metric", "merror"), 
                  ("alpha", 8),
                  ("lambda", 2),
                  ("num_class", 10)]
    num_boost_round = 10000
    early_stopping_rounds = 100
    evals = [(training_data, 'train'), (validation_data, 'validation')]
    boost = xgb.train(params=parameters, 
                    dtrain=training_data, 
                    num_boost_round=num_boost_round, 
                    evals=evals,
                    early_stopping_rounds=early_stopping_rounds, 
                    verbose_eval=False)
    y_pred = boost.predict(validation_data)
    score = sum([prediction == label for prediction, label in zip(y_pred, y_val)]) / len(y_val)
    number_of_iterations = boost.best_iteration
    return score, number_of_iterations

def evaluate(numbers_of_samples: list) -> pd.DataFrame:
    path = generate_path()
    categories = ['Number of labeled samples', 
                  'Number of iterations', 
                  'Accuracy']
    results = pd.DataFrame([], columns=categories)
    for samples in tqdm_notebook(numbers_of_samples):
        print(f'Number of samples: {samples}')
        np.random.seed(seed=seed)
        accuracy, number_of_iterations = training(number_of_training_samples=samples)
        results_of_this_run = pd.Series([samples, number_of_iterations, accuracy], index=categories)
        results = results.append(results_of_this_run, ignore_index=True)
    results.to_csv(f'{path}/results.csv')   
    return results

number_of_samples = [60000,50000,30000,10000,6000,1000,600,100]
results = evaluate(number_of_samples)

Wir erhalten die folgenden Ergebnisse:

Number of labeled samples	Number of iterations	Accuracy
60,000	343	0.9734
50,000	450	0.9724
30,000	469	0.9656
10,000	309	0.9449
6,000	247	0.9287
1,000	197	0.8400
600	392	0.8080
100	323	0.3488

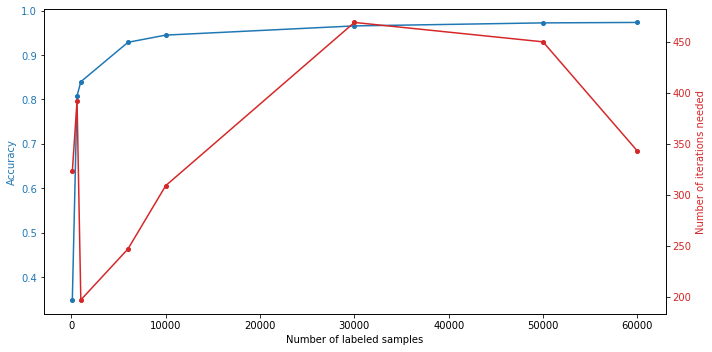
Wie wir sehen, können gute Ergebnisse über 80% bereits mit weniger als 1% der maximalen Anzahl von Trainingsbildern und über 90% mit nur 10% erreicht werden. Dennoch, je mehr Bilder, desto höher die erzielte Genauigkeit.

Schlussfolgerung

Wir haben gezeigt, dass man manchmal überwachtes Lernen mit unüberwachtem Lernen nachahmen und sich einfach auf nicht gekennzeichnete Daten verlassen kann. Die Ergebnisse waren jedoch viel schlechter als bei gekennzeichneten Daten.

Was die Menge der Trainingsdaten betrifft, so haben wir gesehen, dass man für die Klassifikation handschriftlicher Ziffern nicht 60.000 Bilder benötigt. Ab einer bestimmten Stichprobengröße gibt es wahrscheinlich bessere Dinge mit Ihrer Zeit zu tun als mit dem Labeling, z.B. Hyperparameter-Tuning. Aber es ist immer gut, mehr Daten zu haben, und die Anzahl der Bilder, die Sie benötigen, hängt stark von dem Problem ab. Falls Sie ein Problem bei der Umsetzung Ihres Machine Learning Projektes haben, können sie unseren kostenlosen Machine Learning Experten-Talk buchen.