Visual Transformers: Wie eine NLP-Architektur auf Computer Vision angewendet wird

Wir rufen zunächst die Grundbausteine des Transformers in Erinnerung. Wenn Sie bereits mit der Architektur vertraut sind, können Sie zum nächsten Abschnitt übergehen.

Encoder / Decoder

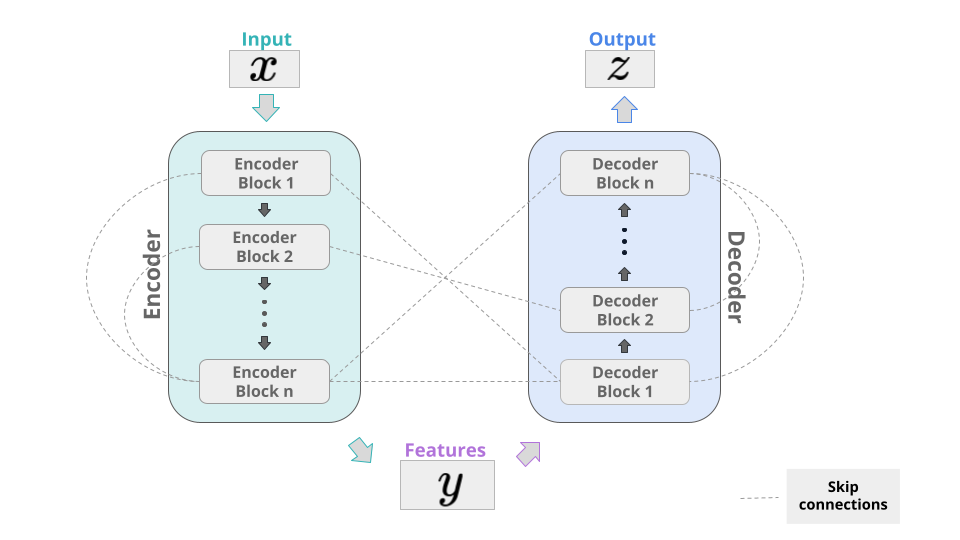
Wie viele andere erfolgreiche Deep-Learning-Modelle besteht auch der Transformer aus einem Encoder- und einem Decoder-Teil. Die allgemeine Idee besteht darin, einige Features eines Eingabevektors zu kodieren und dann diese Merkmale auf eine Ausgabe abzubilden und die relevanten Informationen daraus zu dekodieren. Indem man verschiedene Schichten durch Skip-Verbindungen verbindet, hat das resultierende Modell mehr Informationen in jeder Schicht zur Verfügung und man verhindert auch das "Vanishing Gradient"-Problem. Im Transformer bestehen Encoder und Decoder aus einer Reihe von identischen Blöcken, die sich hauptsächlich auf den Attention-Mechanismus stützen. Die Beispiele, die wir hier behandeln werden, wie das berühmte BERT-Modell, verwenden nur den Encoder-Teil.

Attention

Der Attention-Mechanismus ist das Herzstück für den Erfolg des Transformers. Er ermöglicht dem Modell zu verstehen, welche Teile der Eingabe wichtig sind und wie relevant jeder Teil der Eingabe für andere Teile ist. Konzeptionell aktualisiert eine Self-Attention-Schicht eine Eingabesequenz, indem sie für jeden Eintrag globale Informationen über die gesamte Sequenz einbezieht. Was sie so effizient macht, ist, dass sie dies nicht sequentiell tut, sondern alles auf einmal. Wie LSTM-Netze ermöglicht der Transformer also die natürliche Modellierung weitreichender Abhängigkeiten. Im Gegensatz zu diesen ist er jedoch für die Parallelisierung geeignet und ermöglicht somit effiziente Implementierungen. Für eine Erklärung, wie der Attention-Mechanismus berechnet wird, schauen Sie sich diesen exzellenten Blog-Artikel, unser Webinar über neuronale Sprachmodelle oder das bereits erwähnte Paper Attention is all you need an.

Tokens / Einbettungen

Transformer-basierte Modelle im Bereich NLP, wie BERT, haben ein festes Vokabular. Jedes Element dieses Vokabulars wird als Token bezeichnet. Die Größe dieses Vokabulars kann von Modell zu Modell variieren. Für BERT-base-uncased besteht es aus 30.522 Token. Beachten Sie, wie im Codebeispiel unten einige Wörter durch den Tokenizer aufgespaltet werden. Für verschiedene Modelle kann die Eingabe auf unterschiedliche Weise tokenisiert werden. In diesem Codeschnipsel importieren wir ein BERT-Modell aus der großartigen Bibliothek huggingface transformers.

Diese Token werden von der Einbettungsschicht, die während des Trainings des Modells erlernt wird, auf Vektoren in einem hochdimensionalen Vektorraum (768 oder 1.024 sind gängige Werte für die Einbettungsdimension) abgebildet. Während der Propagierung durch die folgenden Encoder-Blöcke werden die resultierenden Vektordarstellungen durch den Attention-Mechanismus oder Varianten davon (wie Multi-Head-Attention) und das Herstellen von Kontext aktualisiert.

Bei Bildern, die bereits mit einer numerischen Repräsentation versehen sind, wird die Einbettungsschicht obsolet und man muss sich auch nicht um eine feste Vokabulargröße kümmern. Allerdings haben wir noch nicht erklärt, wie man ein Bild, das typischerweise als Matrix dargestellt wird, in eine Folge von Vektoren umwandelt. Wir werden uns nun ein paar verschiedene Möglichkeiten ansehen, dies zu tun.

Bevor wir einen Blick auf den Prozess der Tokenisierung von Bildern werfen, lassen Sie uns mit einem kurzen Exkurs über Convolutional Neural Networks (CNNs) beginnen.

Das Paradigma der Pixel-Konvolution

Eine weit verbreitete und bis heute sehr erfolgreiche Technik im Bereich Computer Vision ist es, Konvolutionsschichten auf ein Bild anzuwenden und so genannte Feature-Maps zu erzeugen. Berühmte Modelle wie das ResNet und seine Nachfolger folgen diesem Ansatz. Typischerweise iteriert man dieses Verfahren auf folgende Weise: Angenommen, die Eingabe ist ein Bild in $$\mathbb{R}^{512 \times 512 \times 3}$$, also ein Bild der Größe $$512 \times 512$$ mit $$3$$ Farbkanälen. In einem ersten Schritt könnte man $$8 \ (3 \times 3)$$ Faltungskerne anwenden, so dass die Ausgabe in $$\mathbb{R}^{512 \times 512 \times 8}$$ erfolgt (die genaue Größe der Feature-Maps kann sich um einige Pixel unterscheiden, je nachdem, ob wir uns entscheiden, die Kanten des Bildes aufzufüllen oder nicht). In einem zweiten Schritt könnte man $$16 \ (3 \times 3)$$ Kernel mit Techniken zur Reduzierung der Dimensionalität (wie Pooling) anwenden, so dass die Ausgabe ein Element von $$\mathbb{R}^{256 \times 256 \times 16}$$ werden würde. Der allgemeine Konsens ist, dass man mit zunehmender Tiefe des Netzes immer mehr Feature-Maps von immer geringerer Größe hinzufügen sollte.

Die gängige Ansicht ist, dass Feature-Maps, die tiefer im Netzwerk liegen, eher High-Level-Merkmale repräsentieren, wie z. B. Formen eines bestimmten Objekts, während Feature-Maps, die näher am Eingang liegen, Low-Level-Merkmale repräsentieren, wie z. B. Kanten. Obwohl es sich gezeigt hat, dass dieser Ansatz der tiefen voll-konvolutionalen neuronalen Netzwerke sehr erfolgreich ist, hat er drei große Nachteile:

1. Jedes Pixel wird gleich behandelt. Das bedeutet, dass Konvolutionen alle Bildbereiche unabhängig von ihrer Bedeutung und ihrem Kontext innerhalb des Bildes verarbeiten. Dies führt zu einer rechnerischen Ineffizienz, da die relevanten Informationen oft in einem kleinen Teil des Bildes konzentriert sind.

2. Die meisten High-Level-Features sind nur in einem kleinen Anteil aller Bilder vorhanden. Schon das ResNet18, die "kleinste" Version dieses Modells, hat auf seiner untersten Ebene bis zu 512 Feature-Maps. Für die meisten Bilder sind wahrscheinlich nur wenige dieser Feature-Maps für die Ausgabe relevant, jedoch werden alle für jedes Bild berechnet, was ebenfalls zu einer rechnerischen Ineffizienz führt.

3. Für eine Konvolution ist es nicht natürlich, räumlich entfernte Konzepte in Beziehung zu setzen. Es liegt in der Natur der Sache, dass eine Konvolution nur Informationen von Pixeln in der Nähe eines Pixels berücksichtigt. Durch das Stapeln mehrerer Konvolutionsschichten kann sich die Information langsam durch ein Bild ausbreiten und Techniken wie größere Kernel oder dilatierte Konvolutionen ermöglichen es auch, weit voneinander entfernte Regionen in Beziehung zu setzen. Dies führt jedoch zu einer sehr großen Anzahl von Parametern und einer hohen Komplexität, selbst wenn die Aufgabe einfach ist.

Um dies zu überwinden, springt der Attention-Mechanismus ein. Schauen wir uns ein paar verschiedene Möglichkeiten an, wie dies geschehen kann.

Tokenisieren durch Patchen

Eine eher naive Art, Token zu erzeugen, ist es, das Bild einfach in kleinere Bereiche zu zerlegen, diese in Vektoren zu verflachen ("Flattening") und voilá - hier haben Sie Ihre Token. Der Vision Transformer (ViT) macht genau das - mit einer zusätzlichen Transformation nach dem Flattening, um die Dimension der Token zu reduzieren, und einer Positionskodierung, die für Transformers üblich ist. Das Coole an dieser Idee ist, dass sie überhaupt nicht auf andere Architekturen (insbesondere CNNs) angewiesen ist - Attention is all you need. Konkret funktioniert das Verfahren wie folgt: Nehmen wir an, wir haben ein $$512 \times 512$$ Bild mit $$3$$ Farbkanälen. Bei einer festen Patch-Größe von $$16 \times 16$$ würde dies zu $$N = 1024$$ Patches führen. Nun ist jeder Patch immer noch eine Matrix (eigentlich sogar ein Rang-3-Tensor) der Dimension $$\mathbb{R}^{16 \times 16 \times 3}$$, aber wir können einfach alle Einträge in einem Vektor der Länge $$16^2 \cdot 3 = 768$$ stapeln (was zufällig auch die Größe der Token-Einbettungen im ursprünglichen BERT-Modell ist). Die Autoren wenden nun eine (lernbare) lineare Transformation an, um die Dimensionalität der resultierenden Folge von Vektoren zu reduzieren und die Token zu erhalten, dies ist jedoch optional.

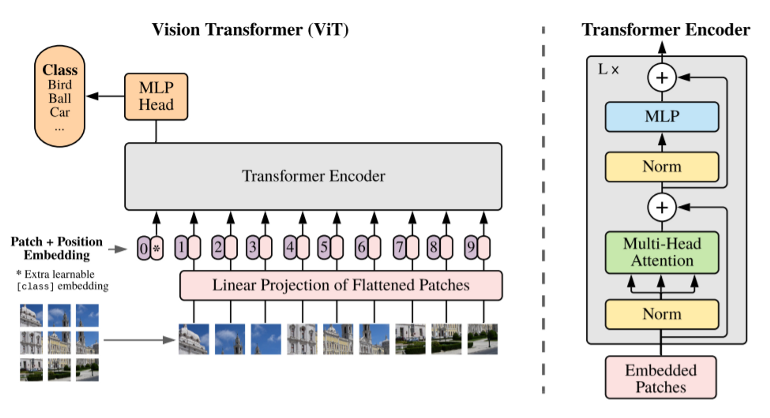
Die Ersteller des ViT verwenden es für die Klassifizierung, wobei nur der Encoder-Teil verwendet wird und, wie im BERT-Modell, ein Klassifizierungs-Token hinzugefügt wird. In der Ausgabeschicht erfolgt die Klassifikation auf Basis dieses Tokens. Weitere Anwendungen sind das Weiterverarbeiten der Ausgabe durch einen Decoder, um Regressionsaufgaben oder Segmentierungen durchzuführen. Bemerkenswert ist, dass das ViT überhaupt keine Konvolutionen verwendet und trotzdem bei anspruchsvollen Datensätzen gut abschneidet. Diese gute Leistung hat allerdings ihren Preis: Man benötigt sehr, sehr große Datenmengen (und Zeit und Ressourcen), wie es bei Transformer-basierten Architekturen üblich ist. Das ViT wurde für die Bildklassifikation auf dem JFT-Datensatz trainiert, der aus über 300 Millionen Bildern besteht, bevor es auf ImageNet mit seinen 1,3 Millionen Bildern "feinjustiert" wurde. Eine ausführliche Diskussion über die Leistung des ViT bei CV-Benchmarks finden Sie in dem Paper.

Sie können auch einen gebrauchsfertigen, vortrainierten ViT in der Transformers-Bibliothek finden.

Da man sich nur auf Transformer und Attention verlassen kann, wenn man unglaublich große Datensätze hat, schauen wir uns an, wie man den Ansatz mit Konvolutionen kombinieren kann, um das Beste aus beiden Welten zu haben.

Erzeugen von Token aus Feature-Maps

Eine solche Architektur ist der Visual Transformer (VT), der nicht mit dem Vision Transformer (ViT) verwechselt werden darf! Er erzeugt Token auf die folgende Weise:

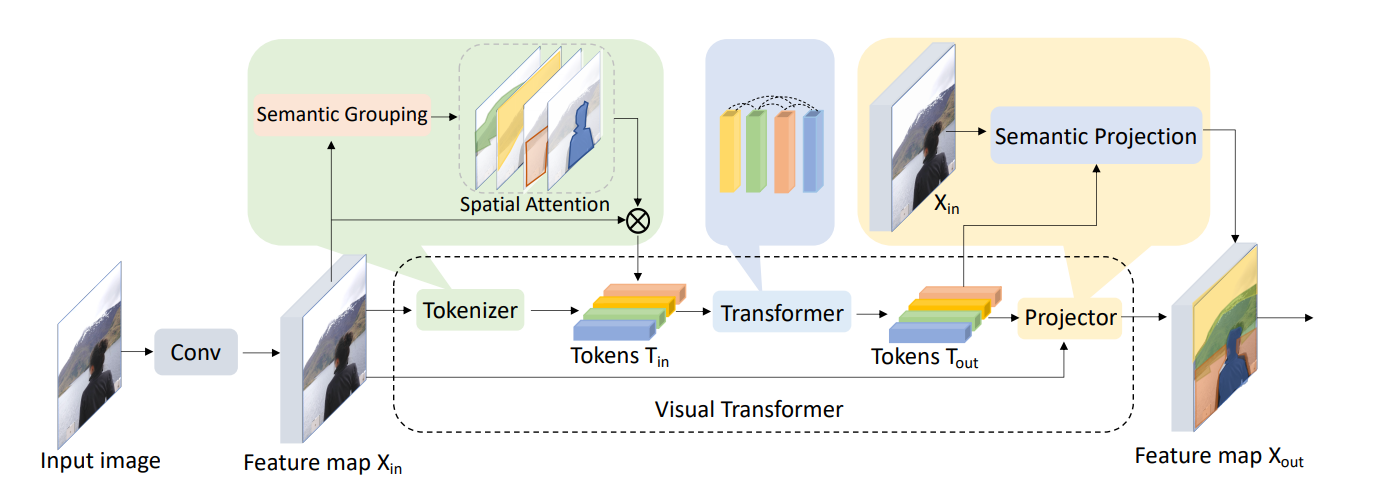
Zunächst werden Konvolutionsschichten angewendet, um einige Low-Level-Merkmale aus dem Eingabebild zu extrahieren. Anschließend wird ein Tokenizer auf die Feature-Maps angewendet, um die Pixel in visuelle Token zu gruppieren. Diese Token durchlaufen einen regulären Transformer, um Beziehungen zwischen den Token zu modellieren. Ihre aktualisierten Repräsentationen können dann direkt für die Klassifizierung verwendet werden, oder sie werden zurück auf die Feature-Map projiziert, um eine semantische Segmentierung durchzuführen. Der für mich interessanteste Teil ist, wie der Tokenizer funktioniert, also schauen wir uns das mal genauer an.

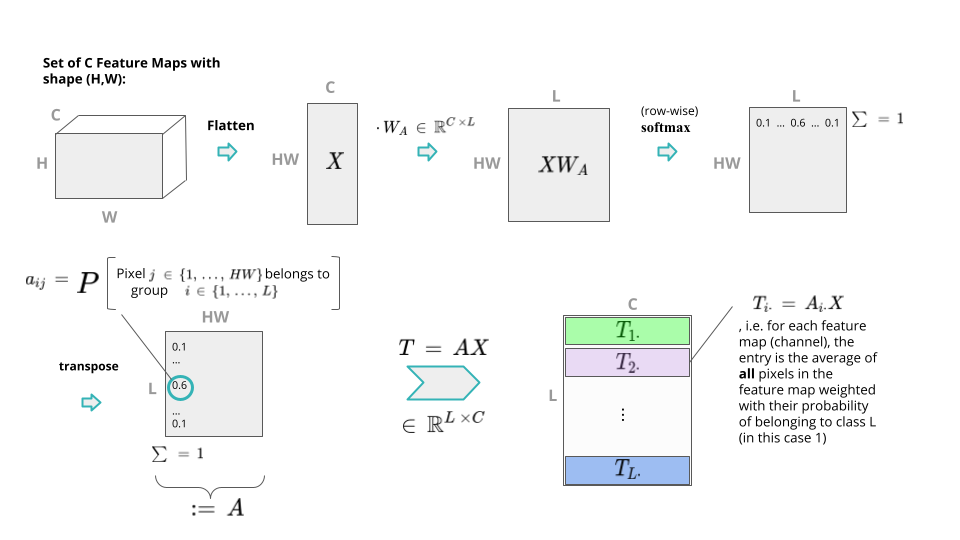
Der Prozess besteht aus mehreren Schritten. Gegeben eine Menge von $$C$$ Feature-Maps in $$\mathbb{R}^{H \times W}$$ (Höhe $$H$$, Breite $$W$$), verflacht man sie zunächst und arrangiert sie in einer 2D-Matrix $$X \in \mathbb{R}^{HW \times C}$$ ein. Nun wird eine lernbare Matrix $$W_A \in \mathbb{R}^{C \times L}$$ von rechts mit $$X$$ multipliziert, um $$L$$ semantische Gruppen zu bilden. Durch Anwendung einer (zeilenweisen) softmax-Operation erhält man eine Matrix, die in jeder Zeile (d.h. Pixel der ursprünglichen Feature-Map) eine Wahrscheinlichkeitsverteilung über die $$L$$ semantischen Gruppen trägt. Multipliziert man nun $$X$$ von links mit der Transponierung dieser Matrix, so ist für jede der $$L$$ Zeilen in der resultierenden Matrix $$T$$ jeder Eintrag der gewichtete Durchschnitt über alle Pixel der ursprünglichen Feature-Map, wobei die Pixel mit ihren Wahrscheinlichkeiten der Zugehörigkeit zur semantischen Gruppe $$l \in L$$ gewichtet werden. Dies ist in der folgenden Abbildung dargestellt:

Also formal:

wobei die Autoren argumentieren, dass $$L$$ viel kleiner als $$HW$$ gewählt werden kann, was die Komplexität des Modells reduziert. Dieser Prozess der Tokenisierung wird auch als Berechnung der räumlichen Attention bezeichnet. Indem man die Token auf ihre Positionen im Bild zurückprojiziert, kann man visualisieren, wie die semantischen Gruppen aussehen. Beachten Sie, wie unterschiedliche Token unterschiedliche semantische Konzepte in den Bildern hervorheben (rote Werte sind hoch, blaue Werte sind niedrig).

In den vorgestellten Experimenten untersuchten die Autoren den Einfluss der Anzahl der Token ($$L$$) auf die Leistung ihres Modells. Sie betrachteten $$L = 16$$, $$32$$ und $$64$$ und überraschenderweise stieg die Leistung mit einer größeren Anzahl von Token nur geringfügig an. Bei Verwendung eines ResNet-34-Backbones zur Erstellung der Feature-Maps war die Top1-Genauigkeit im ImageNet für $$L = 16$$ sogar höher als für größere Werte. Ein Bild kann also tatsächlich durch eine kleine Anzahl von visuellen Token repräsentiert werden, so scheint es zumindest.

Der VT erzielt bei verschiedenen Benchmarks im Bereich Computer Vision großartige Ergebnisse und übertrifft fast immer ihre Konvolution-Pendants, obwohl sie weniger Parameter hat. Im Vergleich zum Vision Transformer benötigt er sehr wenig Zeit und Daten zum Trainieren (er wurde nur auf ImageNet trainiert, das immerhin über eine Million Bilder enthält).

Eine detaillierte Bewertung der Performance finden Sie im Paper.

Um diesen Artikel abzuschließen, lassen Sie uns noch einmal die wichtigsten Punkte in Erinnerung rufen:

• Transformers wurden ursprünglich eingeführt, um NLP-Aufgaben zu bewältigen.

• Für eine lange Zeit (und bis heute) waren Konvolutionen das Standardwerkzeug für Computer Vision. Diese haben jedoch ihre Tücken, wie z. B. das Problem, räumlich entfernte Pixel zueinander in Beziehung zu setzen und einige Aufgaben "übermäßig zu verkomplizieren".

• Zusammen mit Konvolutionen, oder auch ohne sie, kann der Transformer erfolgreich im Bereich Computer Vision eingesetzt werden. Lässt man die Konvolutionen komplett weg, werden enorme Datenmengen und Rechenressourcen benötigt.

• Wir haben uns 2 konkrete Beispiele angeschaut und was es bedeuten kann, ein Bild zu tokenisieren.

• Wenn Sie allgemein mit Transformers experimentieren wollen, ist die Bibliothek huggingface transformers ein guter Anfang. Das Paket timm (torch image models) bietet ebenfalls Implementierungen von Transformatoren für Computer Vision-Aufgaben.

Natürlich haben wir nur an der Oberfläche der Anwendungen von Transformers in diesem Bereich gekratzt. Wenn Sie neugierig auf mehr sind, sehen Sie sich diese Übersicht über Transformer im Bereich Computer Vision an.