Semantische Segmentierung von Satellitenbildern
Dr. Nelson Martins

Dieser Beitrag stellt einige wichtige Erkenntnisse aus unserer Arbeit zur Identifizierung von Dächern auf Satellitenbildern vor. Unser Ziel war es, ein Planungswerkzeug für die Platzierung von Solarmodulen auf Dächern zu entwickeln. Zu diesem Zweck haben wir ein Machine Learning-Modell erstellt, das diese Bilder präzise in verschiedene Arten von Dachteilen und Hintergrund unterteilt. Wir haben gelernt, dass das UNet-Modell mit Würfelkoeffizientenverlust und einer Pixelgewichtungsstrategie Kreuzentropie-basierte Verlustfunktionen bei der semantischen Segmentierung von Satellitenbildern deutlich übertrifft.
Die folgende idealisierte Pipeline veranschaulicht die Funktionalität des Planungstools:
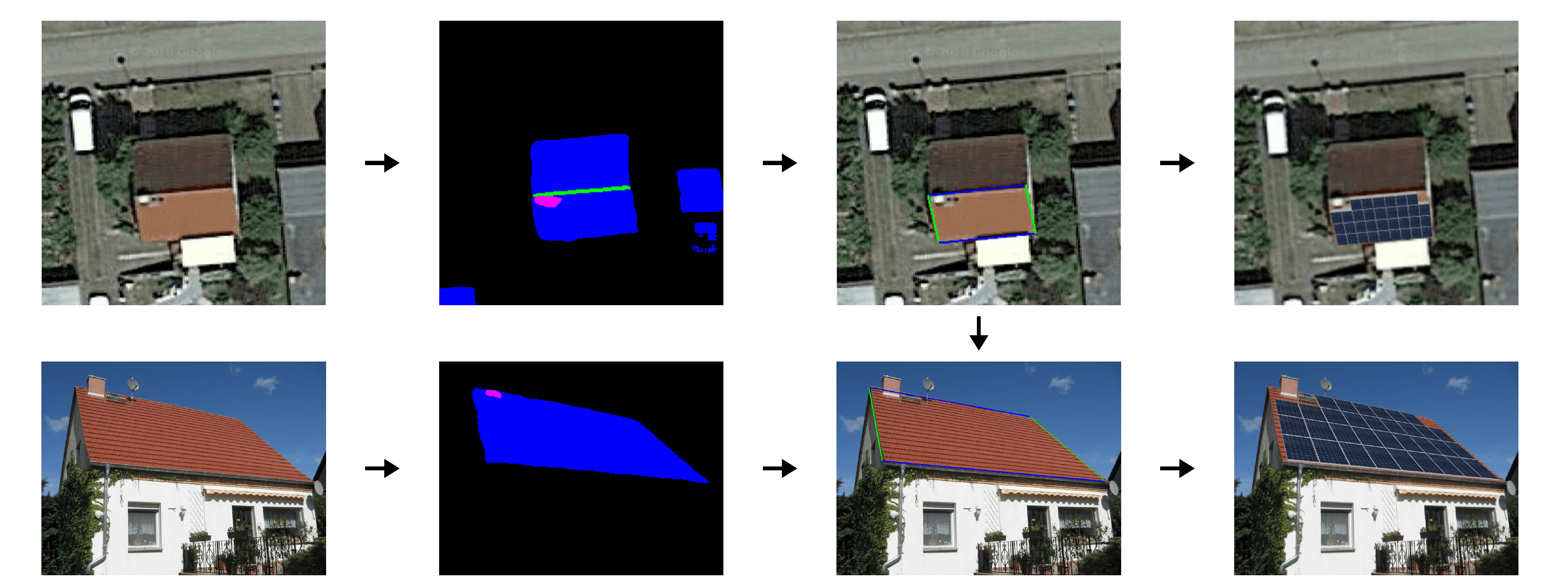
Satellite Image Segmentation
Datensatz
Um das vorgeschlagene Ziel zu erreichen, haben wir eine Datenbank mit Satellitenbildern und den entsprechenden Dach-Annotierungen erstellt. Mit der Google Maps API wurden insgesamt 1500 unterschiedliche Bilder von Häusern in ganz Deutschland gesammelt. Die API akzeptiert als Eingabe einen Wert für Breitengrad und Längengrad, der einen bestimmten Bereich auf dem Globus identifiziert, und einen Satz von Parametern, um die gewünschten Eigenschaften des zurückgegebenen Bildes auszuwählen. Wir wählten die Parameter so, dass die erhaltenen Bilder die bestmögliche Qualität hatten und die meisten Häuser inklusive eines gewissen Spielraumes in einer einzigen Aufnahme aufgenommen werden konnten:
Image dimensions (RGB) |
Scale |
Zoom level |
Pixel size (m) |
Image size (m) |
|
Value |
400x400x3 |
1 |
20 (max) |
0.086 - 0.102 |
34x34 - 41x41 |
Die Pixelgröße ist entlang der Breite variabel und ihr Wert kann wie folgt berechnet werden:
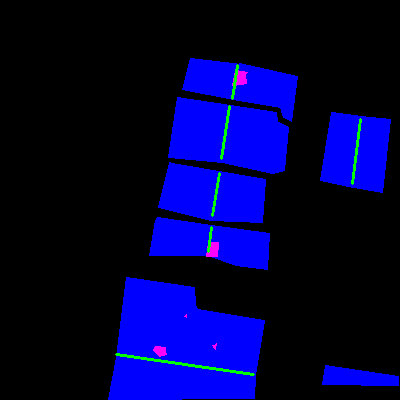
Hier sind einige Beispiele für die Bilder des Datensatzes und ihre jeweiligen Annotierungen:




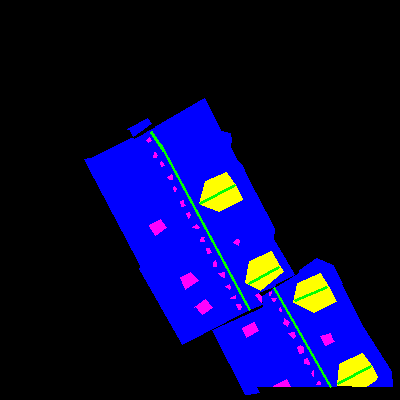
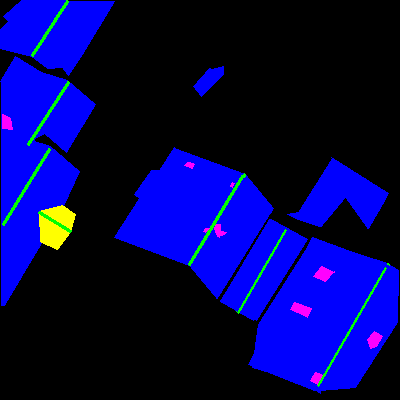
Die Annotierungen sind Dach (blau), Hindernisse (magenta), First (grün) und Gauben (gelb). Die erste dient zur Identifizierung des Bereichs, in dem Solarmodule platziert werden können; die zweite identifiziert Bereiche, in denen Solarmodule nicht platziert werden können, wie Antennen, Schornsteine, Oberlichter; die Firste werden verwendet, um Dachseiten zu trennen und Diskontinuitäten an ihnen zu identifizieren; die Gauben sind ein Sonderfall, wo man nur selten Paneele platzieren würde.
Um das Problem besser zu verstehen, stellen wir auch einige Datenstatistiken vor, die auf diesen 1500 Bildern basieren:
Roof |
Ridge |
Obstacles |
Dormers |
Background |
|
Pixel ratio |
17.74% |
0.70% |
0.70% |
0.92% |
79.93% |
Image ratio |
100.00% |
99.41% |
98.50% |
48.99% |
100.00% |
Der Tabelle können wir Folgendes ablesen:
Die meisten Bilder haben Dächer, Hintergründe, Grate und Hindernisse.
Die meisten Pixel gehören zum Dach oder Hintergrund.
Zu den Graten, Hindernissen und Gauben gehören nur sehr wenige Pixel.
Gauben sind in etwa der Hälfte der Bilder zu finden.
Kurz gesagt: Hohes Klassenungleichgewicht!
Das UNet-Modell
Das vorliegende Problem stellt sich als semantisches Segmentierungsproblem mit hohem Klassenungleichgewicht heraus. Eines der erfolgreichsten Deep-Learning-Modelle für Probleme der Bildsegmentierung ist das UNet-Modell:
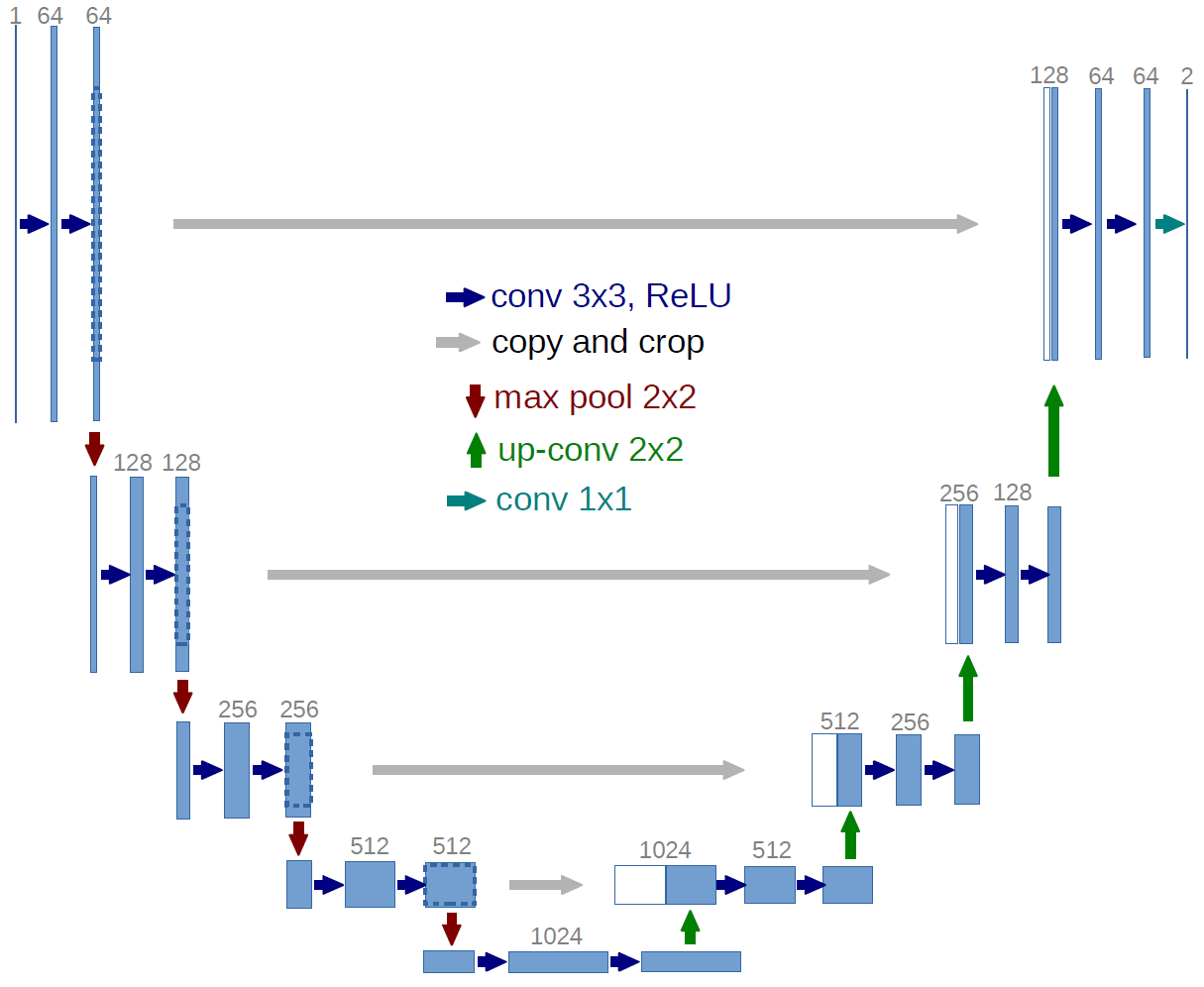
Das UNet ist ein Convolutional Neural Network (CNN), das erstmals für die automatische Segmentierung von Mikroskopie-Zellbildern vorgeschlagen wurde, aber es ist auf jedes Segmentierungsproblem anwendbar. Es besteht aus einem Encoder, gefolgt von einem Decoder. Der Encoder ist für die Erfassung verschiedener Merkmale in verschiedenen Maßstäben verantwortlich und der Decoder verwendet diese Merkmale, um die endgültige Segmentierungskarte zu erstellen. Im UNet-Modell sind der Encoder und der Decoder symmetrisch und auf jeder Stufe mit sogenannten Skip-Layers verbunden. Diese Skip-Layer ermöglichen die Wiederverwendung von Feature-Maps auf jeder Stufe des Decoders, was in der Praxis dazu führt, dass der Segmentierung weitere Details hinzugefügt werden. Das folgende Bild veranschaulicht den Einfluss von Skip-Layers auf die Segmentierungsergebnisse (FCN-32: keine Skip-Layers, FCN-16: ein Skip-Layer, FCN-8: zwei Skip-Layers).
Image source: http://deeplearning.net/tutorial/fcn_2D_segm.html
Original work: https://people.eecs.berkeley.edu/~jonlong/long_shelhamer_fcn.pdf

Tests und Tricks
Unser erster Schwerpunkt lag auf dem Aufbau einer stabilen Pipeline. Zu diesem Zweck haben wir zunächst die Daten nach dem Zufallsprinzip aufgeteilt:
Train set |
Validation set |
Test set |
|
Size |
1100 |
200 |
300 |
Als nächstes implementierten wir das UNet unter Verwendung der Keras API (eine Python Deep Learning-Bibliothek, die u.a. TensorFlow nutzt) und nahmen einige Anpassungen vor:
Batch-Normalisierung nach allen Conv2D-Schichten hinzugefügt
Conv2D-Aktivierung auf selu geändert
Die Batch-Normalisierung ist bekannt für die Verbesserung des Konvergenzprozesses und der Geschwindigkeit, da sie ein übermäßiges Steigen der Tensorwerte verhindert. Dies trägt auch dazu bei, das Netzwerkgewicht unter Kontrolle zu halten, da die Merkmalswerte immer in der gleichen Größenordnung gehalten werden.
Die skalierte exponentielle lineare Einheit (selu) wurde von Klambauer et al. als selbstnormalisierende Schicht vorgeschlagen, die die häufig verwendete ReLU-Aktivierung erweitert und verbessert:
Die Autoren behaupten, dass der Hauptvorteil dieser Aktivierung darin besteht, dass sie den Mittelwert und die Varianz der vorherigen Schichten beibehält. Darüber hinaus trägt sie dazu bei, das Dying ReLU-Problem (und damit das Verschwinden von Gradienten) zu verhindern, da ihre Ableitung bei negativen Werten von Null verschieden ist. Dieser Arbeit folgten andere, die eine Verbesserung der Trainings und der Ergebnisse gezeigt haben. Unsere Vorversuche bestätigten diese Ergebnisse und so entschieden wir uns für ihren Einsatz.
Wir haben auch Datenaugmentation verwendet:
Klappen (auf-abwärts, links-rechts)
Drehungen (+/- 20º)
Intensitätsskalierung
Gauß'sches Rauschen
Schließlich wurden die Trainingshyperparameter empirisch mit dem greedy-Algorithmus ermittelt:
Lernrate: 0.001
Batchgröße: 8
Aktivierung: Sigmoid
Verlust: Würfel + Pixelgewichtung
Optimierer: Adamax
Lernraten-Scheduler: 50% Rückgang nach 20 Epochen ohne Verbesserung
Alle diese Parameter spielten eine wichtige Rolle im Trainingsprozess, aber die richtige Wahl der Verlustfunktion erwies sich als entscheidend.
Verlustfunktionen
Wir haben die klassengewichtete kategorische Kreuzentropie (wcce) und die Würfelverlustfunktionen getestet.
Klassen-gewichtete kategorische Kreuzentropie:
Für ein Bild mit $$ d1 \times d2 $$ Pixeln und $$ K $$ Klassen ist die gewichtete Klasse kategorische Kreuzentropie definiert als
where
Die wcce-Verlustfunktion erzwingt, dass das Modell für positive Klassen einen Wahrscheinlichkeitswert nahe 1 ausgibt. Darüber hinaus hat jede Klasse ein Gewicht $$ w_k $$ zugeordnet, um ihre Bedeutung zu kontrollieren. Das Klassengewicht wurde so festgelegt, dass die Erkennung von Grat, Hindernissen und Gauben erzwungen wird:
Roof |
Ridge |
Obstacles |
Dormers |
Background |
0.2 |
0.3 |
0.25 |
0.25 |
0.05 |
Würfelverlust:
In der gleichen Situation wie oben, ist der Würfelverlust definiert als
wobei
Matrizen sind, die die Vorhersagen für alle Pixel in Bezug auf nur die Klasse k bzw. die Grundwahrheit enthalten und
d.h. das elementweise Produkt.
Der Würfelverlust ist eine kontinuierliche Annäherung an den bekannten Würfelkoeffizienten. In unserem Fall haben wir den Würfelverlust für jede Klasse berechnet und die Ergebnisse über alle Klassen gemittelt. Auf diese Weise sind wir in der Lage, das Klassenungleichgewicht natürlich zu berücksichtigen, ohne eine Klassengewichtung hinzuzufügen.
Mit diesen beiden Verlustfunktionen konnten wir zufriedenstellende Ergebnisse erzielen, aber wir fanden heraus, dass wir es durch die Bestrafung der häufigsten Klasse (Hintergrund) versäumt haben, einige sehr wichtige Pixel zu klassifizieren: diejenigen, die zum Hintergrund zwischen sehr engen Dächern gehören. Aus diesem Grund haben wir uns entschieden, dem Vorschlag von Olaf Ronneberger, et al. zu folgen und eine Pixelgewichtungskomponente hinzuzufügen. Auf diese Weise können wir sicherstellen, dass einige bestimmte Regionen auf dem Bild wichtiger sind als andere.
Pixelgewichtung:
wobei $$ c_1 $$ der Abstand zur Grenze des nächstgelegenen und $$ c_2 $$ zur Grenze des zweitgelegenen Daches ist.
Die folgenden Bilder zeigen, wie die Pixelgewichtung Bereiche zwischen benachbarten Dächern hervorhebt:


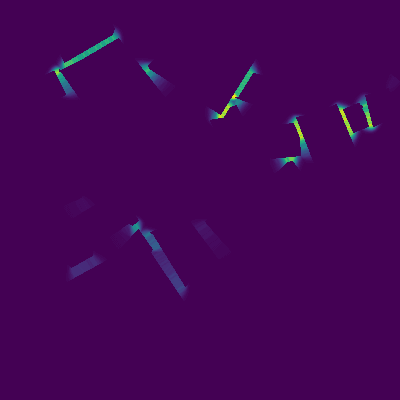





Die Pixelgewichtung wurde wie folgt zum wcce- und Würfelverlust hinzugefügt:
Klassen- und pixelgewichtete Kreuzentropie:
Pixelgewichteter Würfelverlust:
wobei $$ \text{wmse} $$ die gewichtete mittlere quadratische Abweichung ist:
Mit dieser Strategie können wir die Segmentierungsergebnisse sowohl auf Klassen- als auch auf Pixelebene steuern, indem wir die Verlustfunktion nach Wunsch anpassen. Als nächstes präsentieren wir einige der erzielten Ergebnisse.
Ergebnisse
Dies sind die Diagramme des mittleren Würfelkoeffizienten, der während des Trainings für die beschriebenen Verlustfunktionen erhalten wurde:

wcce führt zu besseren Ergebnissen auf dem Trainingsset, aber schlechteren auf dem Validierungsset, was darauf hindeutet, dass es nicht so gut verallgemeinert wie der Würfelverlust. Die Pixelgewichtung pw veränderte die Trainingsplots nicht sehr stark, aber auf dem Validierungsset beschleunigte sich die Konvergenz des Würfelverlustes.
Dies sind die Ergebnisse auf dem Testset, klassenweise:
wcce |
wcce + pw |
dice |
dice + pw |
|
Roof |
0.66 |
0.66 |
0.78 |
0.80 |
Ridge |
0.26 |
0.30 |
0.42 |
0.43 |
Obstacles |
0.34 |
0.38 |
0.52 |
0.51 |
Dormers |
0.27 |
0.50 |
0.64 |
0.68 |
Ground |
0.94 |
0.92 |
0.96 |
0.96 |
Bei der Betrachtung der Ergebnisse ist klar, dass der Würfelverlust die wcce übertroffen hat und dass die Hinzunahme der Pixelgewichtung die Ergebnisse bei beiden verbessert hat, so dass Würfel + pw die beste Kombination von Verlustfunktionen sind.
Schließlich sind hier einige der resultierenden vorhergesagten Segmentierungen (links: originale Satellitenbilder, Mitte: Vorhersagen nach Modell mit Würfelverlust, rechts: Vorhersagen nach Modell mit gewichtetem Würfelverlust):









Aus den visuellen Ergebnissen lässt sich erkennen, dass die Einbeziehung der Pixelgewichtung bei sehr eng beieinander liegenden Dächern zu besserer Dachabtrennung führte.
Kontakt
Wenn Sie mit uns über dieses Thema sprechen möchten, kontaktieren Sie uns gerne und wir melden uns im Anschluss für ein unverbindliches Erstgespräch.
