Understanding and converting MGRS coordinates in Python

Tiago Sanona

Transverse mercator meridian stripes

Working with satellite data, one needs to understand and possibly convert the coordinates the data is given in. Sometimes, especially if released by official bodies, satellite data is provided in MGRS tiles, which are derived from the UTM coordinate system. For example, this is true for Sentinel-2 tiles.

I want to answer the following three questions in this post, using the Python libraries mgrs and pyproj:

  1. What is the difference between MGRS and UTM?

  2. To which MGRS tile does a certain point referenced in latitude and longitude degrees belong to?

  3. How can I express a MGRS tile in Lat/Lon coordinates?

Before we answer these questions, let's first look into what MGRS is.

UTM and MGRS

In order to understand MGRS we first need to talk about UTM.

UTM (Universal Transverse Mercator) is a coordinate system for the surface of the earth. It works by dividing the globe into 60 meridian wise strips and then projecting them using the transverse Mercator projection. Then at intervals of 8º, these zones are further subdivided, parallel wise, into tiles designated by a number between 1 and 60 and a letter of the latin alphabet, for example "33U".

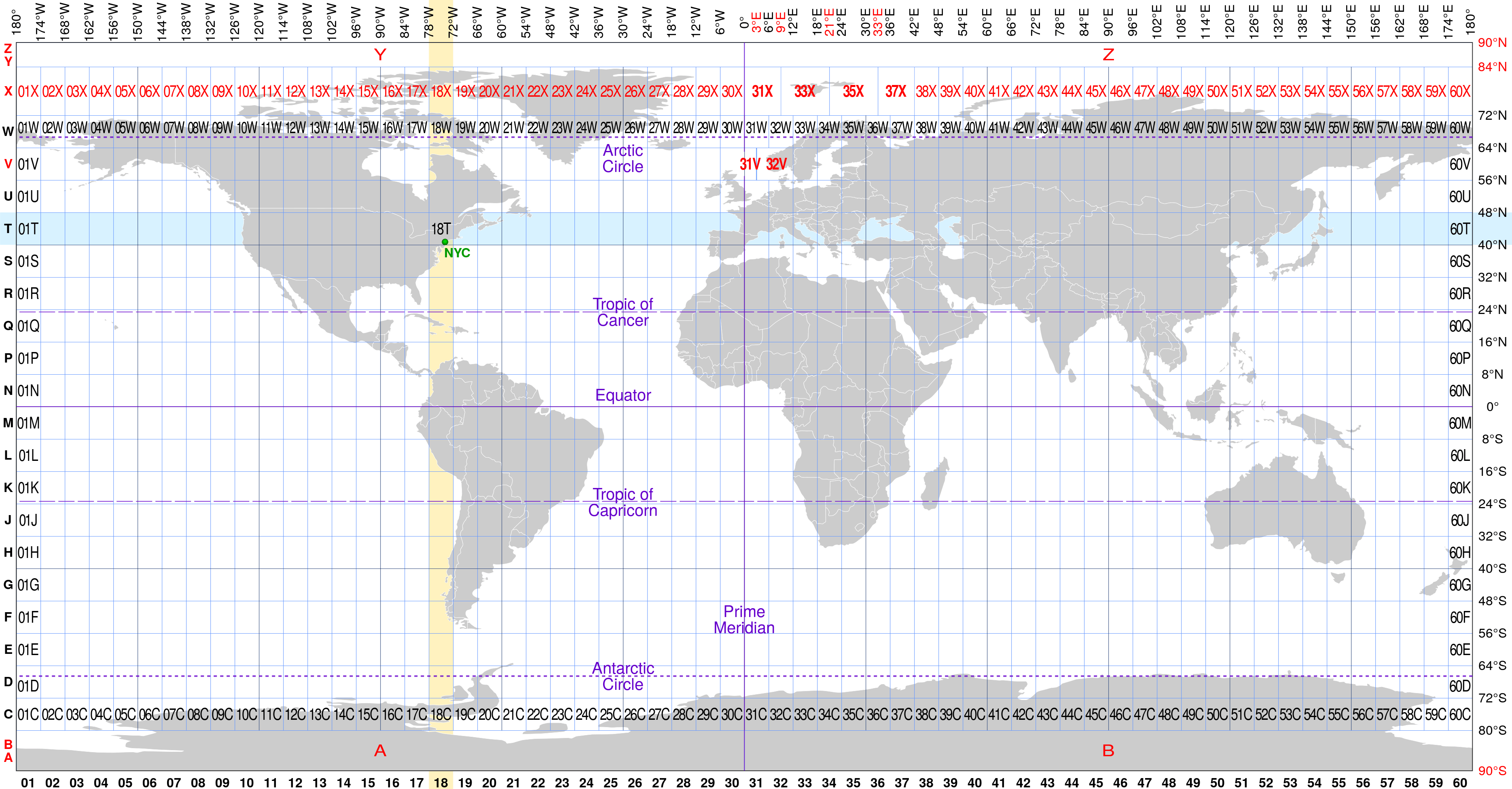
This is the basis of MGRS (Military Grid Reference System). MGRS builds up on UTM by first subdividing each of these tiles into 100km tiles. We identify those smaller tiles with a pair of letters, e.g. "WT".

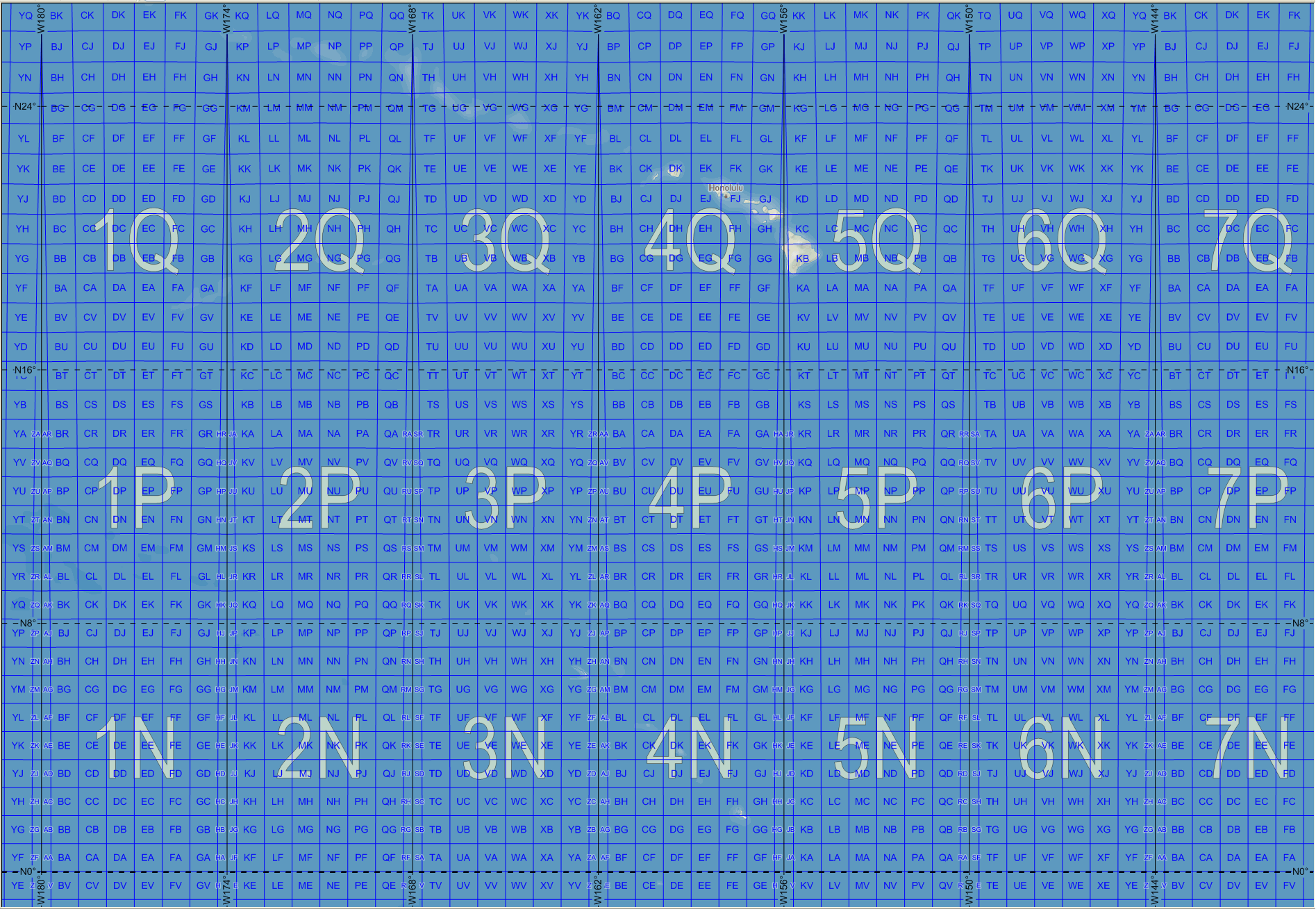
Example of MGRS tiles with 100km precision on top of UTM tiles

It is worth noting that UTM tiles don’t align perfectly with the 100km, so two different names can represent the same tile, for example 3PWT and 3QWT are both valid coordinates for the same area.

The third part of MGRS coordinates consists of a sequence composed of 10 or less numbers (depending on granularity) where the first and second halves indicate how many meters to the east or north, respectively, of the bottom left corner of the 100km tile a point is. Thus a point with coordinates 3PWT3675328453 is in UTM tile 3P, MGRS 100km tile WT and it is 36753m away from the left and 28453m of the bottom edges of the tile.

If one needs to show less precision the numbers have to be truncated rather than rounded. For example 3PWT3675328453 at a precision of 1000m would be 3PWT3628.

MGRS to Latitude/Longitude

Back to the original questions, the first approach you can take is to try to find MGRS tile shape files. Although they are available, you will quickly realise that it might not be the best way to solve this problem, as you will become dependent on one or more shape files which are heavy and have to be cycled through to find a tile that covers a point.

Fortunately there is a python library called mgrs which solves the second question mentioned above. It’s a very simple library that can convert MGRS coordinates to Lat/Lon coordinates and vice versa, with varying degrees of precision.

The example below shows how to convert the coordinates (12.40, 53.51) to MGRS coordinates with default precision (1m) and 10km precision.

import mgrs

mgrs_object = mgrs.MGRS()

mgrs_object.toMGRS(12.40, 53.51)
# returns '39PYP7290672069'

mgrs_object.toMGRS(12.40, 53.51, MGRSPrecision=1)
# returns '39PYP77'

Now to answer the third question, "How can I express a MGRS tile in Lat/Lon coordinates". 

First, you need to find out the location in degrees of the left lower corner of the tile. The .toLatLon method of the same library returns exactly that.

Next, since the tiles have (almost always) constant dimensions, to define a tile in Lat/Lon coordinates you only need to find the coordinates of the upper right corner. To do so, you can use the library pyproj that has a function that given two points in degrees returns the distance between them.

After finding the value to convert between meters and Lon/Lat (x_var and y_var), you can easily find the upper coordinates of the tile but adding to the lower ones the height and width corresponding to the precision of the tile you want, converted into degrees.

import pyproj

geod = pyproj.Geod(ellps='WGS84')

lat_min, lon_min = mgrs_object.toLatLon(mgrs_id)

x_var = geod.line_length([lon_min, lon_min], [lat_min, lat_min + 1])
y_var = geod.line_length([lon_min, lon_min + 1], [lat_min, lat_min])

lat_max = lat_min + mgrs_tile_edge_size / x_var
lon_max = lon_min + mgrs_tile_edge_size / y_var

The drawback of this method is that it assumes that all MGRS tiles are equal, which it is not always true. For these zones, a tile bigger than the real one is returned.

Conclusion

Coordinate reference systems are an important aspect of remote sensing data, thus being able to convert between the various types that exist is fundamental.

In this post I have given an introduction on how MGRS (and UTM) work and how to use the mgrs library from python to convert from MGRS coordinates to Latitude/Longitude in degrees and vice versa.

I also showed a way to obtain the coordinates (of the left lower and upper right corners) of the MGRS tiles based on its name, independently of precision, which is useful if one wants to retrieve entire MGRS tiles from a remote sensing source where queries are made with GPS coordinates.