Bridging Discrete and Continuous State Spaces: Exploring the Ehrenfest Process in Time-Continuous Diffusion Models

---

International Conference on Machine Learning (ICML)

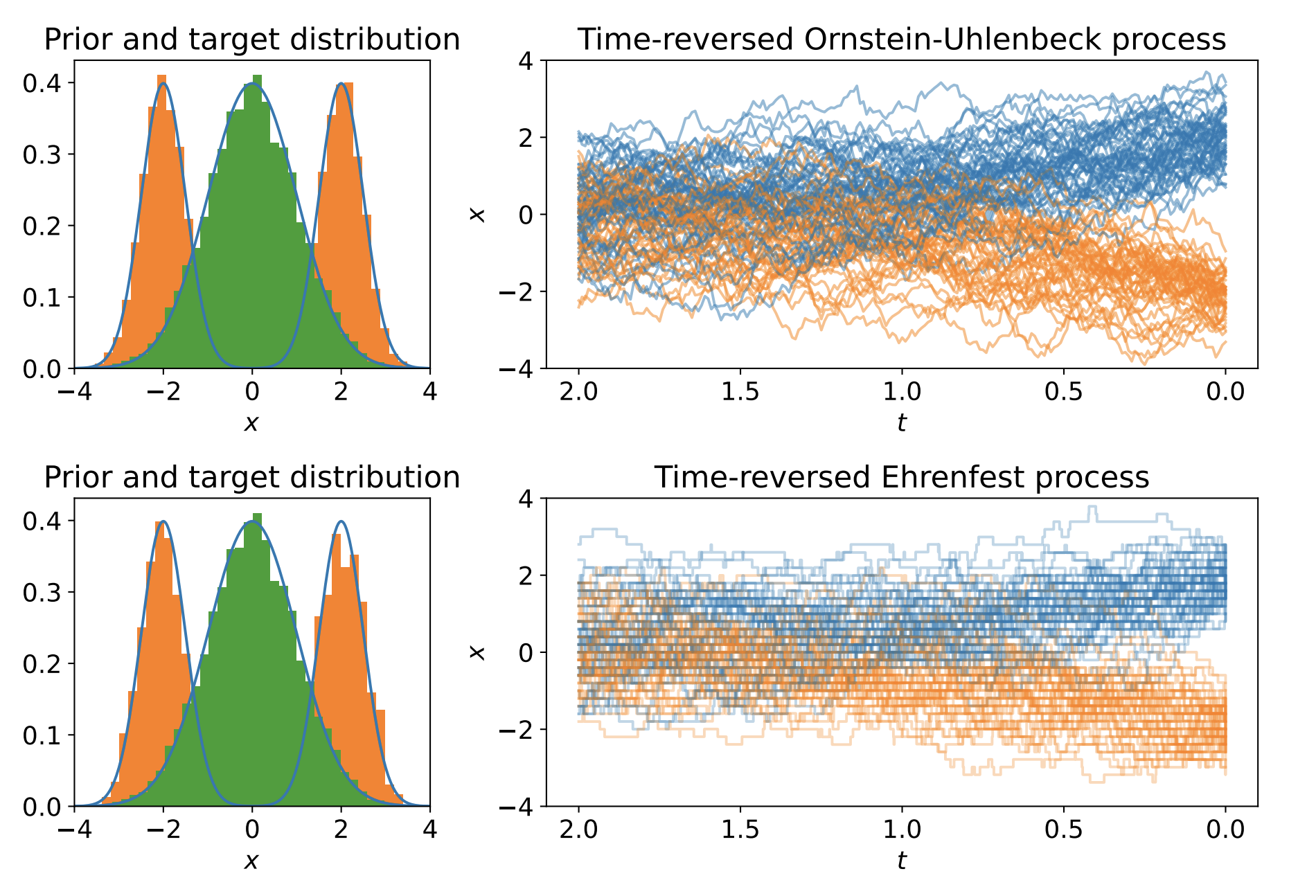
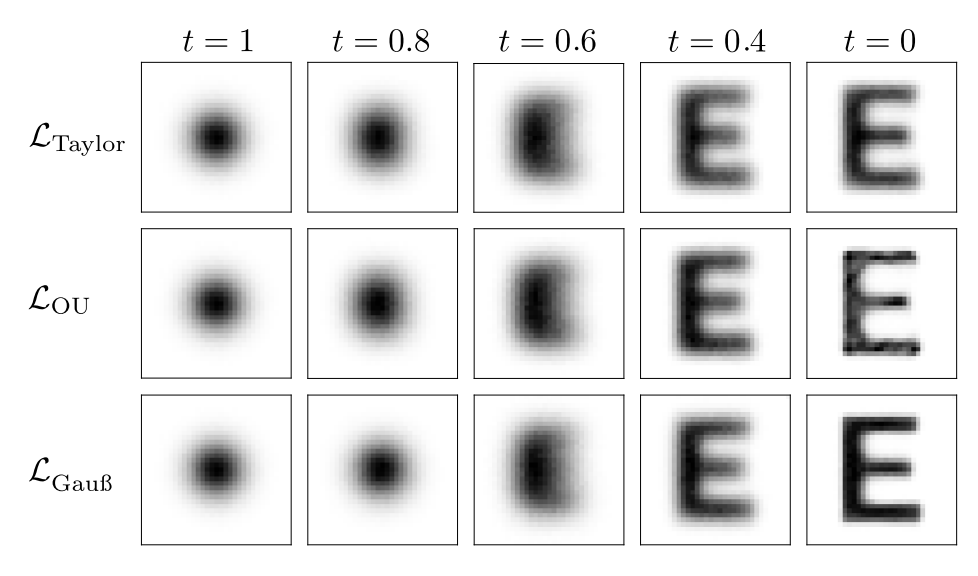
Generative modeling via stochastic processes has led to remarkable empirical results as well as to recent advances in their theoretical understanding. In principle, both space and time of the processes can be discrete or continuous. In this work, we study time-continuous Markov jump processes on discrete state spaces and investigate their correspondence to state-continuous diffusion processes given by SDEs. In particular, we revisit the Ehrenfest process, which converges to an Ornstein-Uhlenbeck process in the infinite state space limit. Likewise, we can show that the timereversal of the Ehrenfest process converges to the time-reversed Ornstein-Uhlenbeck process. This observation bridges discrete and continuous state spaces and allows to carry over methods from one to the respective other setting. Additionally, we suggest an algorithm for training the time-reversal of Markov jump processes which relies on conditional expectations and can thus be directly related to denoising score matching. We demonstrate our methods in multiple convincing numerical experiments.