Mit X-ROCKET zum Mond
Felix Brunner

Dies sind die Reisen des Encodermodells X-ROCKET. Seine fortwährende Mission: fremde, neue Zeitreihen zu erforschen; neue Erklärungen und neue Interpretationen zu finden; kühn nach Bedeutung zu suchen, wo noch niemand zuvor gesucht hat. In den vorangegangenen Teilen dieser Serie haben wir uns in Teil eins mit den Grundlagen der Zeitreihenklassifizierung beschäftigt und in Teil zwei gelernt, wie X-ROCKET funktioniert. Aber genug geredet, jetzt ist es an der Zeit, die X-ROCKET-Motoren anzuwerfen und dieses Modell in Aktion zu sehen. Lasst uns loslegen!
Bereiten Sie sich auf den Abflug vor!
Wir werden den Datensatz "AsphaltPavementTypeCoordinates" von Souza (2018) als Beispiel verwenden. Dieser Datensatz besteht aus 2.111 Beispielen von Beschleunigungsmessdaten, die von Autos aufgezeichnet wurden, die über verschiedene Arten von Straßenbelägen fuhren. Jedes Zeitreihenbeispiel im Datensatz hat drei Kanäle (entsprechend der X-, Y- und Z-Richtung), von denen jeder mit 100 Hz gemessen wird. Die Länge der Aufzeichnungen variiert von 66 Zeitbeobachtungen bis zu 2.371. Die Klassen sind "flexibel" (38,6 %), "Kopfsteinpflaster" (25,0 %) und "unbefestigte Straße" (36,4 %). Laut Beschreibung erreichte das beste Modell eine Genauigkeit von 80,66% bei dieser Aufgabe, die wir als Benchmark verwenden werden. Houston, wir haben also unser Problem - ein relativ ausgewogenes dreifaches multivariates Zeitreihenklassifizierungsproblem, um genau zu sein.
Das Modul aeon bietet eine einfache Möglichkeit, diesen Datensatz für unsere maschinelle Lernaufgabe zu laden. Wir werden auch scikit-learn verwenden, um den Originalautoren zu folgen und den vollständigen Datensatz in gleich große Trainings- und Test-Splits zu unterteilen:
from aeon.datasets import load_classification
from sklearn.model_selection import train_test_split
X, y, meta = load_classification("AsphaltPavementTypeCoordinates")
X_train, X_test, y_train, y_test = train_test_split(
X, z, test_size=0.5, random_state=0
)Wie man eine ROCKET baut
Als Nächstes wollen wir ein geeignetes Gefäß zur Kodierung dieses Datensatzes zusammenstellen. Nachdem wir das Modul xrocket mit seinen Abhängigkeiten in unserer Umgebung installiert haben, können wir sofort das vollständige Encoder-Modul importieren. Dann müssen wir nur noch eine Instanz davon mit geeigneten Parametern für unser Problem initialisieren. Da unser Datensatz drei Kanäle hat, ist die Wahl von in_channels klar. Da die Länge der Zeitreihen innerhalb unseres Datensatzes stark variiert, ist es sinnvoll, max_kernel_span auf einen Wert zu setzen, der auch für die kürzeren Beispiele geeignet ist, in diesem Fall also auf 100. Schließlich belassen wir combination_order und feature_cap vorerst auf den Standardwerten von eins und 10.000:
from xrocket import XRocket
encoder = XRocket(
in_channels=3,
max_kernel_span=100,
combination_order=1,
feature_cap=10_000,
)Angesichts dieser Eingaben wird unser Encoder automatisch so eingestellt, dass er die üblichen 84 MiniROCKET-Kernel bei 12 verschiedenen Dilatationswerten hat. Bei drei Datenkanälen wählt X-ROCKET drei Pooling-Schwellenwerte für jede Kernel-Dilatations-Kanal-Kombination, um innerhalb der feature_cap zu bleiben. Daher beträgt die Einbettungsdimension 84 12 3 * 3 = 9.072. Um diesen Apparat schließlich zum Einsteigen vorzubereiten, müssen wir nur noch geeignete Werte für die 9.072 Pooling-Schwellenwerte finden. Wir tun dies, indem wir unsere XRocket-Instanz an ein Datenbeispiel anpassen. Da das Modell mit PyTorch-Tensoren arbeitet, bei denen die erste Dimension für das Stapeln mehrerer Beispiele in einem Stapel reserviert ist, müssen wir die Daten nur von einem 2D-Numpy-Array in einen 3D-Tensor umwandeln und in den Encoder einspeisen:
from torch import Tensor
encoder.fit(Tensor(X_train[0]).unsqueeze(0))Los geht's!
Nun, da unser X-ROCKET kalibriert ist, können wir den Countdown starten. Auch hier müssen die Eingaben im 3D-Tensorformat vorliegen, also müssen wir die Beispiele in PyTorch-Tensoren umwandeln, bevor wir sie an das Modell übergeben. Aufgrund der unterschiedlichen Längen der Zeitreihen können wir nicht so einfach mehrere Beispiele zu einem Stapel zusammenfassen. Daher ist es bequemer, die Beispiele einzeln zu kodieren und die Einbettungen in zwei Listen zu sammeln, eine für die Trainingsmenge und eine für die Testmenge. Zeit für den vollen Schub, viel Erfolg!
embed_train, embed_test = [], []
for x in X_train:
embed_train.append(encoder(Tensor(x).unsqueeze(0)))
for x in X_test:
embed_test.append(encoder(Tensor(x).unsqueeze(0)))8,02 Sekunden auf einer mäßig schnellen Consumer-CPU später sind die Einbettungen sowohl des Trainings- als auch des Testsatzes fertig. Das heißt, wir haben jetzt eine Darstellung der Eingabedaten unterschiedlicher Größe in festdimensionalen Vektoren. Es ist also an der Zeit, aus diesem Problem ein tabellarisches Problem mit benannten Merkmalen zu machen, die in einem DataFrame gespeichert sind. Der Encoder stellt das Attribut feature_names zur Verfügung, das die Namen der einzelnen Einbettungswerte als Tupel von (pattern, dilation, channel, threshold) enthält. Wir legen diese Tupel in einem Index ab und benennen sie entsprechend. Schließlich erstellen wir die Rahmen, um die transformierten Datensätze zu speichern. Wer sagt denn, dass die Klassifizierung von Zeitreihen eine Wissenschaft für sich ist?
from torch import concat
import pandas as pd
feature_names = pd.Index(encoder.feature_names)
df_train = pd.DataFrame(data=concat(embed_train), columns=feature_names)
df_test = pd.DataFrame(data=concat(embed_test), columns=feature_names)X-ROCKET einen Zweck geben
Wie so viele Dinge im Universum kämpft auch X-ROCKET damit, seinen Weg ohne einen Kopf zu finden. Um sicherzustellen, dass es seiner Flugbahn zum vorgesehenen Ziel - der Zeitreihenklassifizierung - folgen kann, müssen wir einen geeigneten Vorhersagekopf finden, der die Nutzlast liefert. Wie bereits erwähnt, ist prinzipiell jedes Vorhersagemodell, das für den beabsichtigten Zweck geeignet ist, in Ordnung. Beachten Sie, dass dies theoretisch auch tiefe neuronale PyTorch Feed-Forward-Netzwerke einschließt, die es ermöglichen, Backpropagation von Ende zu Ende zurück zu den X-ROCKET-Gewichten laufen zu lassen, um ihre Einbettungen zu verbessern. Aber keine Panik, es ist auch ohne Deep Thought möglich, Antworten zu finden! Da wir letztlich an der Erklärbarkeit der Vorhersagen interessiert sind, wählen wir stattdessen ein einfaches und erklärbares Klassifikationsmodell. Der RandomForestClassifier von Scikit-learn ist dafür ein guter Anfang. Wir müssen ihn nur laden und auf unsere Trainingsdaten anwenden:
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(random_state=0)
clf.fit(df_train, y_train)Wow, das ging ja fast ab wie eine Rakete! Nur 3,13 Sekunden später haben wir unseren Klassifikator. Schauen wir mal, wie er sich in dem Datensatz schlägt. Da in der Originalarbeit eine Genauigkeit von 80,66 % angegeben wird, wollen wir unser Modell auf die gleiche Weise mit dem Hold-Out-Datensatz bewerten, wie sie es getan haben:
from sklearn.metrics import accuracy_score
pred_test = clf.predict(df_test)
acc_test = accuracy_score(y_test, pred_test)Und da haben wir es, unser Modell erreicht eine Genauigkeit von 90,19% auf dem Testsatz! Nicht schlecht, aber ist das genug, um einen kleinen Rocket Man stolz zu machen? Um diese Frage schlüssig zu beantworten, sind natürlich genauere Vergleiche erforderlich. Dennoch scheint dies ein erfolgreicher Start gewesen zu sein!
Wo noch kein ROCKET Man zuvor war
Es ist an der Zeit, X-ROCKET auf seiner ultimativen Suche nach Bedeutung bis an die letzte Grenze zu führen. Da das Modell akzeptabel zu funktionieren scheint, ist es sinnvoll, auch die Erklärungen zu analysieren, die es für seine Vorhersagen liefert. Glücklicherweise bietet der von uns gewählte Random-Forest-Klassifikator ein Attribut namens feature_importances_, das allen Merkmalen des Modells Wichtigkeitswerte zuweist. Da wir den entsprechenden Index in feature_names gespeichert haben, können wir die beiden Arrays leicht zusammenführen:
feature_importances = pd.Series(
data=clf.feature_importances_,
index=feature_names,
)Die Analyse dieses Objekts ist ohnehin nur bedingt sinnvoll. Wir können zum Beispiel sehen, dass die wichtigste Einbettung für unser Modell das Muster HLHLLLHLL bei Dilatation zwei im Y-Kanal mit einem Pooling-Schwellenwert von -10,84 ist. Ein H in dem Muster steht für einen hohen Wert, ein L für einen niedrigen, so dass das Muster etwa wie |_|___|__ aussieht. Es ist nun jedoch einfach, die Wichtigkeitswerte zusammenzufassen, um die relative Wichtigkeit z. B. der Eingangskanäle zu untersuchen. Summiert man die einzelnen Kanäle, erhält man die nachstehenden Wichtigkeitswerte. Da X-ROCKET die Zufälligkeit bei der Zusammenstellung der Einbettungen beseitigt, werden aus jedem Kanal und jedem Dilatationswert die gleichen Merkmale extrahiert. Daher bietet der Vergleich der gruppierten Merkmalsbedeutungen auf diese Weise einen fairen Vergleich.
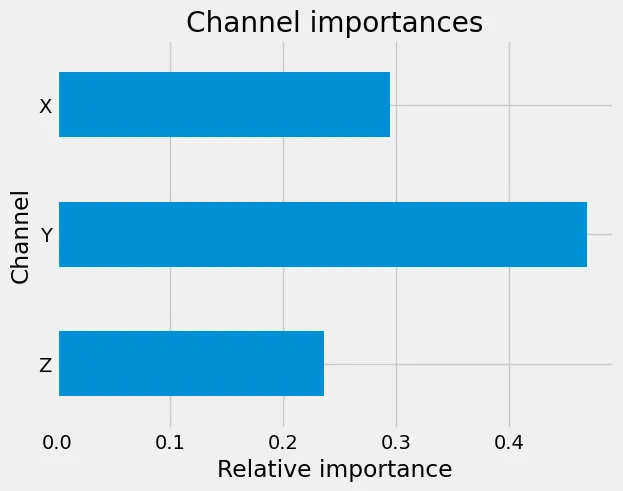
Relative Bedeutung der Eingangskanäle für die Vorhersagen.
Das heißt, der Y-Kanal scheint der klare Favorit zu sein, gefolgt vom X-Kanal. Ähnlich verhält es sich, wenn man die verschiedenen Dilatationswerte zusammenzählt: Es zeigt sich, dass die höheren Frequenzen ausschlaggebend sind. Bei Einträgen, die mit 100 Hz aufgezeichnet werden, bedeutet ein Dilatationswert von 2 zum Beispiel eine Frequenz von 50 Hz. Wie in der nachstehenden Abbildung zu sehen ist, sind die meisten Informationen in diesen höheren Frequenzen enthalten, d. h. in denjenigen mit kleineren Dilatationswerten.
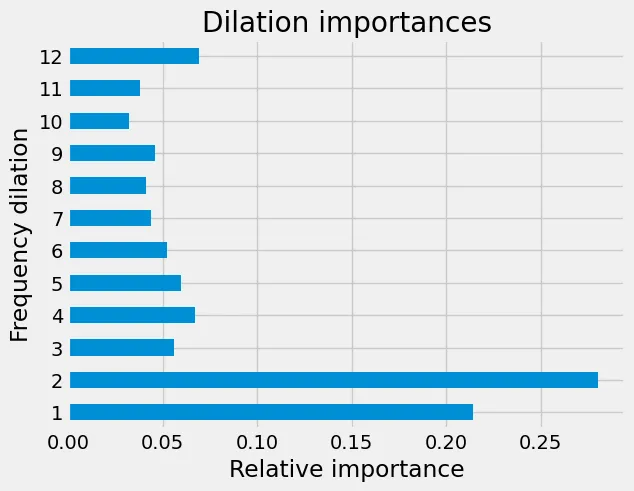
Relative Bedeutung der verschiedenen Frequenzdilatationen für die Vorhersagen.
Was hat der Arzt zur ROCKET gesagt?
"Time to get your booster shot!" Dementsprechend könnte man sich fragen, wie man diesem Raketenschiff einen zusätzlichen Leistungsschub verschaffen könnte. Im Bereich des maschinellen Lernens sind die Möglichkeiten natürlich endlos. Man könnte zum Beispiel alternative Modellköpfe wie Gradient-Boosting-Algorithmen ausprobieren oder die entsprechenden Hyperparameter besser optimieren. Auf einem anderen Weg könnte man darüber nachdenken, wie man die Datenqualität verbessern oder den vorhandenen Datensatz mit künstlichen Beispielen anreichern kann. Dies würde jedoch den Rahmen dieser einfachen Demonstration sprengen. Es wäre jedoch interessant zu sehen, ob der Kodierer weiter verbessert werden kann, um zusätzliche Erkenntnisse über die Einflussfaktoren für die Vorhersagekraft zu gewinnen, wenn neben den bisher gesehenen univariaten auch mehrkanalige Merkmale berücksichtigt werden. Lassen wir also alles unverändert, ändern aber nur den Encoder, indem wir combination_order=2 setzen und die Anzahl der Features mit feature_cap=15_000 bei der Initialisierung von X-ROCKET leicht erhöhen. Die resultierende Einbettung ist nun 12.096-dimensional mit 6 Kanalkombinationen anstelle von nur 3 Kanälen und 2 Pooling-Schwellenwerten für jeden Ausgang.
Neben einem leichten Anstieg der Genauigkeit des Testsatzes auf 91,13%, stellen wir erneut fest, dass der Y-Kanal wieder am wichtigsten zu sein scheint, aber jetzt haben Kombinationen von Y mit den anderen Kanälen eine größere Bedeutung:
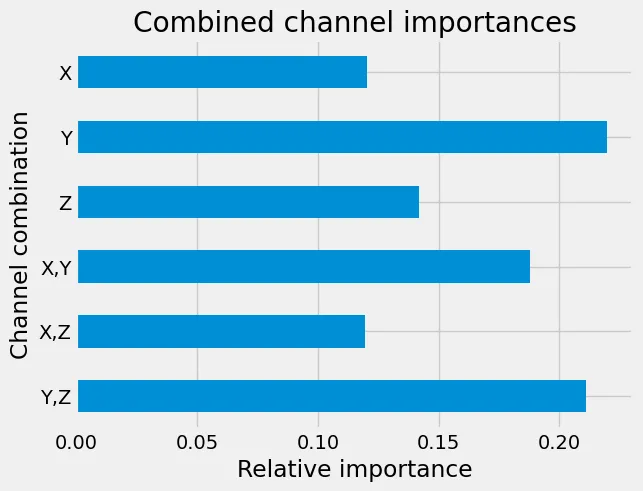
Relative Bedeutung der Eingangskanalkombinationen für die Vorhersagen.
Schlussfolgerungen
In dieser Artikelserie haben wir gesehen, wie ein bestehendes Zeitreihen-Encoder-System umstrukturiert werden kann, um neue Erkenntnisse über die Vorhersagetreiber zu gewinnen. Teil eins hat einige der Fortschritte im maschinellen Lernen für den Zeitreihenbereich beleuchtet. Dann wurde in Teil zwei und in diesem dritten Teil X-ROCKET, ein erklärbarer Zeitreihen-Encoder, sowohl technisch als auch mit einem praktischen Anwendungsbeispiel vorgestellt. Auch wenn dieses Konstrukt im vorliegenden Beispiel seine Aufgabe erfüllt hat, ist es wichtig, darauf hinzuweisen, dass die von X-ROCKET gelieferten Erklärungen nur so gut sind wie die Vorhersagefähigkeiten des Modells für das jeweilige Problem. Das heißt, es hat keinen Sinn, ein Modell zu interpretieren, das in Bezug auf seine Vorhersagen nicht gut genug ist. Es gibt also keine Garantie dafür, dass derselbe Ansatz in verschiedenen Umgebungen gleich gut funktioniert, insbesondere wenn die Eingabedaten wenig Signal enthalten. Nichtsdestotrotz: Raketen sind cool, daran führt kein Weg vorbei!
Referenzen
Dempster, A., Schmidt, D. F., & Webb, G. I. (2021, August). Minirocket: A very fast (almost) deterministic transform for time series classification. In Proceedings of the 27th ACM SIGKDD conference on knowledge discovery & data mining (pp. 248–257).
Souza, V. M. (2018). Asphalt pavement classification using smartphone accelerometer and complexity invariant distance. Engineering Applications of Artificial Intelligence, 74, 198–211.
Dieser Artikel entstand im Rahmen des vom Bundesministerium für Bildung und Forschung (BMBF) unter dem Förderkennzeichen 02P20A501 geförderten Projekts "AI-gent3D - KI-gestütztes, generatives 3D-Drucken" unter Koordination des PTKA Karlsruhe.
